题目内容
在△ABC中,“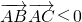 ”是“△ABC是钝角三角形”的
”是“△ABC是钝角三角形”的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
A
分析:由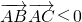 ”可得“△ABC是钝角三角形”,而“△ABC是钝角三角形”推不出角A为钝角,由充要条件的定义可得答案.
”可得“△ABC是钝角三角形”,而“△ABC是钝角三角形”推不出角A为钝角,由充要条件的定义可得答案.
解答:由题意可知若“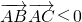 ”则必有角A为钝角,可得“△ABC是钝角三角形”,
”则必有角A为钝角,可得“△ABC是钝角三角形”,
而“△ABC是钝角三角形”不一定角A为钝角,可能角B或C为钝角,故推不出角A为钝角,
故可得“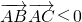 ”是“△ABC是钝角三角形”的充分不必要条件,
”是“△ABC是钝角三角形”的充分不必要条件,
故选A
点评:本题考查充要条件的判断,涉及三角形形状的判断和向量的数量积问题,属基础题.
分析:由
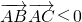 ”可得“△ABC是钝角三角形”,而“△ABC是钝角三角形”推不出角A为钝角,由充要条件的定义可得答案.
”可得“△ABC是钝角三角形”,而“△ABC是钝角三角形”推不出角A为钝角,由充要条件的定义可得答案.解答:由题意可知若“
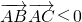 ”则必有角A为钝角,可得“△ABC是钝角三角形”,
”则必有角A为钝角,可得“△ABC是钝角三角形”,而“△ABC是钝角三角形”不一定角A为钝角,可能角B或C为钝角,故推不出角A为钝角,
故可得“
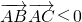 ”是“△ABC是钝角三角形”的充分不必要条件,
”是“△ABC是钝角三角形”的充分不必要条件,故选A
点评:本题考查充要条件的判断,涉及三角形形状的判断和向量的数量积问题,属基础题.

练习册系列答案
相关题目
在△ABC中,tanA是第3项为-4,第7项为4的等差数列的公差,tanB是第3项为,第6项为9的等比数列的公比,则△ABC是( )
| A、等腰三角形 | B、锐角三角形 | C、直角三角形 | D、钝角三角形 |
在△ABC中,CD是AB边上的高,a2+c2<b2,
+
=1,则( )
| CD2 |
| AC2 |
| CD2 |
| BC2 |
A、A+B=
| ||
B、A-B=
| ||
C、B-A=
| ||
D、|A-B|=
|
 请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.
请考生在第(1),(2),(3)题中任选一题作答,如果多做,则按所做的第一题记分.