题目内容
15.将函数f(x)=3sin(2x+φ),φ∈(0,π)的图象沿x轴向右平移$\frac{π}{6}$个单位长度,得到函数g(x)的图象,若函数g(x)满足g(|x|)=g(x),则φ的值为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:将函数f(x)=3sin(2x+φ),φ∈(0,π)的图象沿x轴向右平移$\frac{π}{6}$个单位长度,
得到函数g(x)=3sin(2x-$\frac{π}{3}$+φ),的图象,若函数g(x)满足g(|x|)=g(x),则g(x)为偶函数,
故-$\frac{π}{3}$+φ=kπ+$\frac{π}{2}$,k∈Z,即φ=kπ+$\frac{5π}{6}$,∴令k=0,可得φ=$\frac{5π}{6}$,
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
5.已知f(x)=4x5+3x4+2x3-x2-x-$\frac{1}{2}$,用秦九韶算法求f(-2)等于( )
| A. | -$\frac{197}{2}$ | B. | $\frac{197}{2}$ | C. | $\frac{183}{2}$ | D. | -$\frac{183}{2}$ |
7.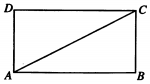 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )
 如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )
如图,在矩形ABCD中,$AB=\sqrt{3},BC=1$,将△ACD沿折起,使得D折起的位置为D1,且D1在平面ABC的射影恰好落在AB上,则直线D1C与平面ABC所成角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |