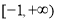题目内容
5.如图,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点A关于直线0B的对称点为C,则$\overrightarrow{OC}$可表示为( )
| A. | $\frac{(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{a}}{|\overrightarrow{b}{|}^{2}}$-$\overrightarrow{b}$ | B. | $\frac{2(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{b}}{|\overrightarrow{b}{|}^{2}}$-$\overrightarrow{a}$ | C. | $\frac{(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{a}}{|\overrightarrow{a}{|}^{2}}$$-\overrightarrow{b}$ | D. | $\frac{2(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{a}}{|\overrightarrow{a}{|}^{2}}$$-\overrightarrow{b}$ |
分析 可以OA,OC为邻边作平行四边形OADC,根据条件可知点D在OB上,从而可以得到$\overrightarrow{OD}=2|\overrightarrow{a}|cos<\overrightarrow{a},\overrightarrow{b}>•\frac{\overrightarrow{b}}{|\overrightarrow{b}|}$,从而根据$\overrightarrow{OC}=\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}$即可表示出向量$\overrightarrow{OC}$.
解答 解:根据条件知:AC⊥OB,且AC被OB平分;
如图,以OA,OC为邻边作平行四边形OADC,则: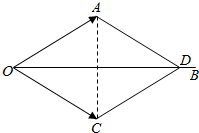
$\overrightarrow{OD}=2|\overrightarrow{a}|cos<\overrightarrow{a},\overrightarrow{b}>•\frac{\overrightarrow{b}}{|\overrightarrow{b}|}$=$2|\overrightarrow{a}|•\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}•\frac{\overrightarrow{b}}{|\overrightarrow{b}|}=\frac{2(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{b}}{|\overrightarrow{b}{|}^{2}}$;
又$\overrightarrow{OC}=\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}$;
∴$\overrightarrow{OC}=\frac{2(\overrightarrow{a}•\overrightarrow{b})\overrightarrow{b}}{|\overrightarrow{b}{|}^{2}}-\overrightarrow{a}$.
故选:B.
点评 考查平行四边形的对角线互相平分,相等向量的概念,以及向量数乘的几何意义,向量夹角余弦的计算公式.

 如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )
如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3}{2}$ |
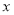 的方程
的方程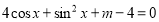 恒有实数解,则实数
恒有实数解,则实数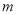 的取值范围是( )
的取值范围是( )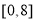 B.
B. 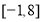 C.
C.  D.
D.