题目内容
等比数列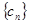 满足
满足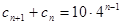 ,
,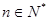 ,数列
,数列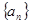 满足
满足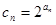
(1)求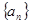 的通项公式;(5分)
的通项公式;(5分)
(2)数列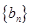 满足
满足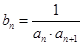 ,
,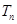 为数列
为数列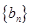 的前
的前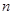 项和.求
项和.求 ;(5分)
;(5分)
(3)是否存在正整数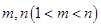 ,使得
,使得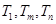 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有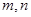 的值;若不存在,请说明理由.(6分)
的值;若不存在,请说明理由.(6分)
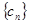 满足
满足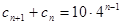 ,
,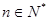 ,数列
,数列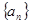 满足
满足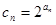
(1)求
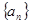 的通项公式;(5分)
的通项公式;(5分)(2)数列
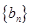 满足
满足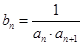 ,
,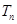 为数列
为数列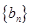 的前
的前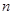 项和.求
项和.求 ;(5分)
;(5分)(3)是否存在正整数
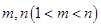 ,使得
,使得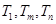 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有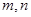 的值;若不存在,请说明理由.(6分)
的值;若不存在,请说明理由.(6分)(1) ;(2)
;(2) =
=
(3)当且仅当 ,
, 时,
时,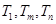 成等比数列。
成等比数列。
 ;(2)
;(2) =
=
(3)当且仅当
 ,
, 时,
时,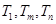 成等比数列。
成等比数列。试题分析:(1)解:
 ,所以公比
,所以公比 2分
2分 计算出
计算出 3分
3分 4分
4分 5分
5分(2)
 6分
6分于是
 8分
8分 =
= 10分
10分(3)假设否存在正整数
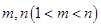 ,使得
,使得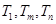 成等比数列,则
成等比数列,则 , 12分
, 12分可得
 ,
, 由分子为正,解得
 ,
, 由
 ,得
,得 ,此时
,此时 ,
, 当且仅当
 ,
, 时,
时,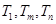 成等比数列。 16分
成等比数列。 16分说明:只有结论,
 ,
, 时,
时,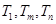 成等比数列。若学生没有说明理由,则只能得 13分
成等比数列。若学生没有说明理由,则只能得 13分点评:综合题,本题综合考查等比数列知识、数列的求和、不等式解法,对考查考生灵活运用数学知识的能力起到了很好的作用。

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,则x的值为( )
,则x的值为( )



 为等比数列,
为等比数列, 为其前
为其前 项和,已知
项和,已知 ,则公比
,则公比



 是公比大于1的等比数列,
是公比大于1的等比数列, 为数列
为数列 项和.已知
项和.已知 ,且
,且 构成等差数列.
构成等差数列. 求数列
求数列 的前
的前 .
. 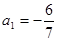 ,
,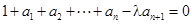 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),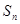 为数列{an}的前
为数列{an}的前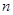 项和.
项和.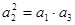 ,求
,求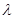 的值;
的值; ;
;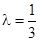 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.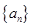 的相邻两项
的相邻两项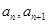 是关于
是关于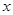 的方程
的方程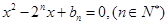 的两根,且
的两根,且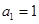
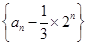 是等比数列;
是等比数列;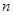 项和
项和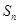 ;
;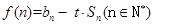 若
若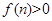 对任意的
对任意的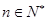 都成立,求
都成立,求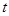 的取值范围。
的取值范围。 的前
的前 项和为
项和为 ,
, ,若数列
,若数列 是公比为
是公比为 的等比数列.
的等比数列.  ;
; ,
, ,求数列
,求数列 的前
的前 .
. 是等比数列,若
是等比数列,若 ,
, ,则
,则 ( )
( )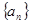 满足
满足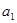 ,
,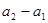 ,
,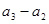 ,…,
,…, 是首项为
是首项为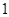 ,公比为
,公比为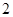 的等比数列,那么
的等比数列,那么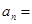 ( )
( )