题目内容
4.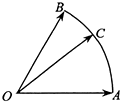 己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{\sqrt{3}}{2}$ |
分析 根据条件对$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$两边平方即可得到x2+xy+y2=1,根据x2+y2≥2xy即可得到xy$≤\frac{1}{3}$,并且x,y>0,从而得到$(x+y)^{2}≤\frac{4}{3}$,这便可求得x+y的最大值.
解答 解:由已知条件,${\overrightarrow{OC}}^{2}=(x\overrightarrow{OA}+y\overrightarrow{OB})^{2}$;
∴1=x2+xy+y2;
∵x2+y2≥2xy;
∴$xy≤\frac{1}{3}$;
根据题意x>0,y>0;
∴$(x+y)^{2}=1+xy≤\frac{4}{3}$;
∴$x+y≤\frac{2\sqrt{3}}{3}$;
∴x+y的最大值为$\frac{2\sqrt{3}}{3}$.
故选:A.
点评 考查向量数量积的计算公式,向量加法的平行四边形法则,共线向量基本定理,以及基本不等式的运用.

练习册系列答案
相关题目
15.已知抛物线的准线方程x=$\frac{1}{2}$,则抛物线的标准方程为( )
| A. | x2=2y | B. | x2=-2y | C. | y2=x | D. | y2=-2x |
12.要得到y=cos2x的图象,可由函数y=cos(2x-$\frac{π}{3}$)的图象( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
13.对于集合A、B,定义A+B={x+y|x∈A,y∈B},下列命题:
①A+B=B+A;
②(A+B)+C=A+(B+C);
③若A+A=B+B,则A=B;
④若A+C=B+C,则A=B.
其中正确的命题是( )
①A+B=B+A;
②(A+B)+C=A+(B+C);
③若A+A=B+B,则A=B;
④若A+C=B+C,则A=B.
其中正确的命题是( )
| A. | ① | B. | ①② | C. | ②③ | D. | ①④ |
14.设平面α⊥平面β,直线a?α,直线b?β,且a⊥b,则( )
| A. | a⊥β | B. | b⊥α | ||
| C. | a⊥β与b⊥α中至少有一个成立 | D. | a⊥β与b⊥α同时成立 |