题目内容
16.在等比数列{an}中,对于任意n∈N*都有an+1a2n=3n,则a1a2…a6=729.分析 通过等比数列的定义及an+1a2n=3n可得公比及a2,利用等比中项的性质计算即可.
解答 解:∵an+1a2n=3n,∴an+2a2(n+1)=3n+1,
∴q3=$\frac{{a}_{n+2}{a}_{2(n+1)}}{{a}_{n+1}{a}_{2n}}$=$\frac{{3}^{n+1}}{{3}^{n}}$=3,即q=$\root{3}{3}$,
∵a2a2=31,∴a2=$\sqrt{3}$,∴a5=${a}_{2}•{q}^{3}$=3$\sqrt{3}$,
∴a2•a5=$\sqrt{3}•3\sqrt{3}$=9,
∴a1a2…a6=(a1•a6)(a2•a5)(a3•a4)=93=729,
故答案为:729.
点评 本题考查求数列前几项的乘积,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴,直线AB交y轴于点P,若$\overrightarrow{AP}$=$\sqrt{2}$$\overrightarrow{PB}$,则椭圆的离心率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
7.某地近几年粮食需求量逐年上升,如表是部分统计数据:
(1)利用所给数据求年需求量与年份之间的回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)利用(1)中所求出的直线方程预测该地2015年的粮食需求量.
(参考公式:$\widehat{b}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}-x)({y}_{1}-y)}{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}-x)^{2}}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}{y}_{1})-nxy}{\underset{\stackrel{n}{∑}}{n+1}{x}_{1}^{2}-n{x}^{2}}$,$\widehat{a}$=$\widehat{y}-\widehat{b}x$)
| 年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
| 年需求量(万吨) | 257 | 276 | 286 | 298 | 318 |
(2)利用(1)中所求出的直线方程预测该地2015年的粮食需求量.
(参考公式:$\widehat{b}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}-x)({y}_{1}-y)}{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}-x)^{2}}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}{y}_{1})-nxy}{\underset{\stackrel{n}{∑}}{n+1}{x}_{1}^{2}-n{x}^{2}}$,$\widehat{a}$=$\widehat{y}-\widehat{b}x$)
4.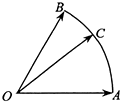 己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
 己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{\sqrt{3}}{2}$ |
11.已知y=sin(x+$\frac{π}{6}$)图象横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),再将图象向右平移$\frac{π}{3}$个单位,则对称轴方程为( )
| A. | x=-$\frac{π}{2}$ | B. | x=-$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=$\frac{π}{4}$ |
1.一几何体的三视图如图所示,则它的体积为( )
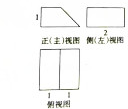

| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
6.4位同学要完成100米的接力跑,要求每个人跑的路程不超过其他任一同学所跑路程的3倍,若某一同学所跑路程为x米,则x的取值范围为( )
| A. | 10≤x≤20 | B. | 10≤x≤30 | C. | 20≤x≤40 | D. | 10≤x≤50 |
 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,PD⊥面ABCD,直线PA与直线BC所成角大小为60°,求直线PB与直线AC所成角的大小.
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,PD⊥面ABCD,直线PA与直线BC所成角大小为60°,求直线PB与直线AC所成角的大小.