题目内容
14.设平面α⊥平面β,直线a?α,直线b?β,且a⊥b,则( )| A. | a⊥β | B. | b⊥α | ||
| C. | a⊥β与b⊥α中至少有一个成立 | D. | a⊥β与b⊥α同时成立 |
分析 本题考查的知识点是平面与平面之间的位置关系,及直线与平面间的位置关系,根据平面α⊥平面β,直线a?α,b?β,a⊥b,不难判断a与β及b与α的关系,进而得到答案
解答 解:若平面α⊥平面β,直线a?α,b?β,a⊥b
①若b垂直平面α与平面β的交线,此时b⊥α,a与β关系不确定;
②若a垂直平面α与平面β的交线,此时a⊥β,b与α关系不确定;
③假设a,b均不垂直于平面α与平面β的交线,
则过b上不在交线上一点O,做平面α与平面β的交线的垂线l,
则l⊥α,则l⊥a,由于l∩b=O,l?β,b?β,则a⊥β
此时a⊥平面α与平面β的交线
这与假设矛盾,故a,b至少有一条与平面α与平面β的交线垂直,
由a⊥β与b⊥α中至少有一个成立;
故选C
点评 本题考查了面面垂直的性质定理以及线面垂直的判定定理的运用;线线垂直可由线面垂直的性质推得;线线关系与线面关系的相互转化是关键.

练习册系列答案
相关题目
4.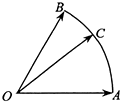 己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
 己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{\sqrt{3}}{2}$ |
9.已知F1,F2分别为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,P为椭圆上一点,且PF2垂直于x轴.若|F1F2|=2|PF2|,则该椭圆的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
19.设S是整数集Z的非空子集,如果?a,b∈Z,都有a2-b2∈S,则称S是一个好集,已知S是一个“好集”,下面命题为假命题的是( )
| A. | 一切奇数都属于S | B. | 偶数4k-2(k∈Z)都不属于S | ||
| C. | 若x,y∈S,则xy∈S | D. | 若x,y属于S,则x+y∈S |
6.4位同学要完成100米的接力跑,要求每个人跑的路程不超过其他任一同学所跑路程的3倍,若某一同学所跑路程为x米,则x的取值范围为( )
| A. | 10≤x≤20 | B. | 10≤x≤30 | C. | 20≤x≤40 | D. | 10≤x≤50 |
5.函数f(x)=sinx•ln(x+1)的图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
 如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,PD⊥面ABCD,直线PA与直线BC所成角大小为60°,求直线PB与直线AC所成角的大小.
如图,四棱锥P-ABCD中,底面ABCD是矩形,AB=4,AD=2,PD⊥面ABCD,直线PA与直线BC所成角大小为60°,求直线PB与直线AC所成角的大小.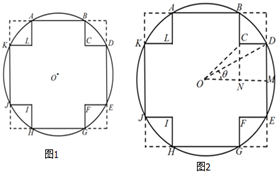 如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)
如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)