题目内容
设t>0,数列{an}是首项为t,公差为2t的等差数列,其前n项和为Sn,若对于任意n∈N*,
>
恒成立,则t的取值范围是______.
| ||
| an |
| 1-t |
∵数列{an}是首项为t,公差为2t的等差数列
∴an=t+(n-1)×2t=2tn-t
∴Sn=
=
=tn2
∴
=
=
>
对于任意n∈N*恒成立,
即(
)min>
令g(n)=
,g'(n)=
=
<0
∴g(n)=
在[1,+∞)为单调减函数,则当n→∞时,g(n)→
∴
≥
,且t>0解得0<t≤1
故答案为:0<t≤1
∴an=t+(n-1)×2t=2tn-t
∴Sn=
| (a1+an)n |
| 2 |
| (t+2tn-t)n |
| 2 |
∴
| ||
| an |
| ||
| 2tn-t |
| n | ||||
2
|
| 1-t |
即(
| n |
| 2n-1 |
| (1-t)t |
令g(n)=
| n |
| 2n-1 |
| 2n-1-2n |
| (2n-1)2 |
| -1 |
| (2n-1)2 |
∴g(n)=
| n |
| 2n-1 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| (1-t)t |
故答案为:0<t≤1

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
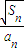 >
>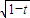 恒成立,则t的取值范围是 .
恒成立,则t的取值范围是 .