题目内容
设t>0,数列{an}是首项为t,公差为2t的等差数列,其前n项和为Sn,若对于任意n∈N*,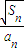 >
>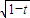 恒成立,则t的取值范围是 .
恒成立,则t的取值范围是 .
【答案】分析:先求出数列的通项公式和前n项和,然后将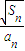 =
=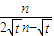 >
>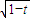 对于任意n∈N*恒成立转化成
对于任意n∈N*恒成立转化成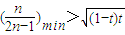 ,然后令g(n)=
,然后令g(n)=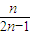 ,然后利用导数研究函数的单调性,从而求出g(n)>
,然后利用导数研究函数的单调性,从而求出g(n)> ,从而得到关于t的不等式,解之即可,注意定义域.
,从而得到关于t的不等式,解之即可,注意定义域.
解答:解:∵数列{an}是首项为t,公差为2t的等差数列
∴an=t+(n-1)×2t=2tn-t
∴Sn=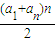 =
=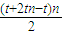 =tn2
=tn2
∴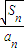 =
=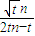 =
=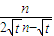 >
>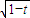 对于任意n∈N*恒成立,
对于任意n∈N*恒成立,
即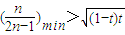
令g(n)=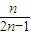 ,g'(n)=
,g'(n)=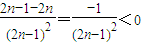
∴g(n)=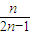 在[1,+∞)为单调减函数,则当n→∞时,g(n)→
在[1,+∞)为单调减函数,则当n→∞时,g(n)→
∴ ≥
≥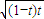 ,且t>0解得0<t≤1
,且t>0解得0<t≤1
故答案为:0<t≤1
点评:本题主要考查了等差数列的通项与求和,以及恒成立问题和数列与不等式的综合,同时考查了转化的思想,以及利用导数研究函数的单调性,属于中档题.
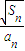 =
=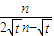 >
>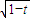 对于任意n∈N*恒成立转化成
对于任意n∈N*恒成立转化成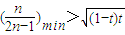 ,然后令g(n)=
,然后令g(n)=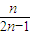 ,然后利用导数研究函数的单调性,从而求出g(n)>
,然后利用导数研究函数的单调性,从而求出g(n)> ,从而得到关于t的不等式,解之即可,注意定义域.
,从而得到关于t的不等式,解之即可,注意定义域.解答:解:∵数列{an}是首项为t,公差为2t的等差数列
∴an=t+(n-1)×2t=2tn-t
∴Sn=
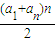 =
=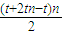 =tn2
=tn2∴
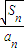 =
=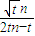 =
=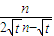 >
>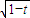 对于任意n∈N*恒成立,
对于任意n∈N*恒成立,即
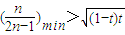
令g(n)=
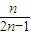 ,g'(n)=
,g'(n)=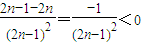
∴g(n)=
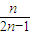 在[1,+∞)为单调减函数,则当n→∞时,g(n)→
在[1,+∞)为单调减函数,则当n→∞时,g(n)→
∴
 ≥
≥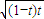 ,且t>0解得0<t≤1
,且t>0解得0<t≤1故答案为:0<t≤1
点评:本题主要考查了等差数列的通项与求和,以及恒成立问题和数列与不等式的综合,同时考查了转化的思想,以及利用导数研究函数的单调性,属于中档题.

练习册系列答案
相关题目