题目内容
已知函数
(ω＞0)的图象与直线y＝－2的两个相邻公共点之间的距离等于π，则
的单调递减区间是( )
A． | B． |
C． | D． |
A
解析试题分析：因为
最小值为－2，可知y＝－2与f(x)两个相邻公共点之间的距离就是一个周期，于是
，即ω＝2，即
令
，k∈Z，解得x∈，选A
考点：三角函数恒等变形，三角函数的图象及周期、最值、单调性.
练习册系列答案
名校课堂系列答案
相关题目
已知
，则tan
的值是
A． | B． | C． | D． |
若函数
（
），又
，
，且
的最小值为
，则正数
的值是（ ）
A． | B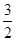． | C． | D． |
一扇形的中心角为2，对应的弧长为4，则此扇形的面积为（ ）.
| A．1 | B．2 | C．4 | D．8 |
的值为
A． | B． | C． | D． |
将函数y＝cos2x的图象向右平移
个单位长度，再将所得图象的所有点的横坐标伸长到原来的2倍（纵坐标不变），得到的函数解析式为（ ）.
| A．y＝sinx | B．y＝－cos4x | C．y＝sin4x | D．y＝cosx |
函数
的值域为
A． | B． | C． | D． |
函数
的部分图象如图所示，点
、
是最高点，点
是最低点．若△
是直角三角形（C为直角），则
的值为
A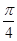． | B． | C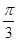． | D． |
为了得到函数y=cos(x+
)的图象，只需把余弦曲线y=cosx上的所有的点 ( )
| A．向左平移个单位长度 | B．向右平移个单位长度 |
C．向左平移 个单位长度 | D．向右平移个单位长度 |