Question

如图，在四棱锥S—ABCD中，底面ABCD，底面ABCD是矩形，且，E是SA的中点。

   （1）求证：平面BED平面SAB；

   （2）求直线SA与平面BED所成角的大小。

Answer 1

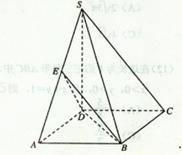
解：

（Ⅰ）∵SD⊥平面ABCD，∴平面SAD⊥平面ABCD，

∵AB⊥AD，∴AB⊥平面SAD，∴DE⊥AB．                                                 …3分

∵SD＝AD，E是SA的中点，∴DE⊥SA，

∵AB∩SA＝A，∴DE⊥平面SAB

∴平面BED⊥平面SAB．                                                                       …6分

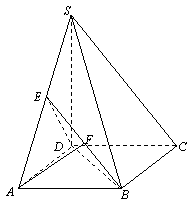
（Ⅱ）作AF⊥BE，垂足为F．

由（Ⅰ），平面BED⊥平面SAB，则AF⊥平面BED，

则∠AEF是直线SA与平面BED所成的角．                                           …8分

设AD＝2a，则AB＝a，SA＝2a，AE＝a，

△ABE是等腰直角三角形，则AF＝a．

在Rt△AFE中，sin∠AEF＝＝，

故直线SA与平面BED所成角的大小45°．                                               …12分