题目内容
已知数列 中,
中,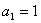 ,
, 且
且
 .
.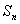 为数列
为数列 的前
的前 项和,且
项和,且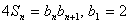
 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项的和
项的和 ;
;
(Ⅲ)证明对一切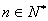 ,有
,有 .
.
解:(I)由已知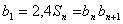 得
得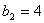 ,
,
 ,
,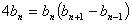 ,
,
由题意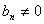 ,即
,即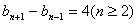 ,
,
当n为奇数时,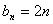 ;当n为偶数时,
;当n为偶数时,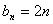 .
.
所以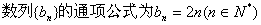 .
.
(Ⅱ)解法一:
由已知,对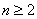 有
有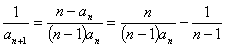 ,
,
两边同除以 ,得
,得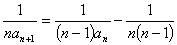 ,
,
即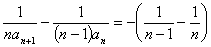 ,
,
于是,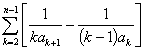 =
=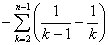 =
=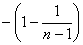 ,
,
即 ,
,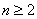 ,所以
,所以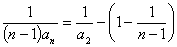 =
=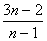 ,
,
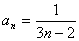 ,
,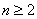 ,又
,又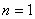 时也成立,故
时也成立,故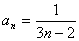 ,
,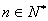 .
.
所以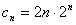 ,
,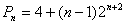
解法二:也可以归纳、猜想得出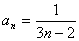 ,然后用数学归纳法证明.
,然后用数学归纳法证明.
(Ⅲ)当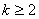 ,有
,有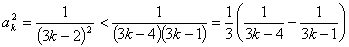 ,
,
所以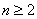 时,有
时,有
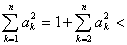
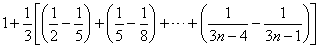
=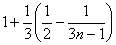
 .
.
当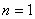 时,
时,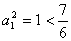 . 故对一切
. 故对一切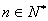 ,有
,有 .
.

练习册系列答案
相关题目
 与圆
与圆 的两个交点始终为圆
的两个交点始终为圆 的轨迹方程为 .
的轨迹方程为 .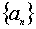
 满足
满足 ,则数列
,则数列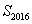 的值是___________.
的值是___________. 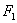 ,
,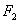 分别是双曲线
分别是双曲线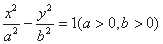 的左、右焦点,若双曲线左支上存在一点
的左、右焦点,若双曲线左支上存在一点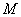 ,使
,使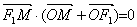 ,
, 为坐标原点,且
为坐标原点,且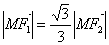 ,则该双曲线的离心率为
,则该双曲线的离心率为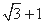 B.
B.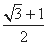 C.
C.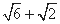 D.
D.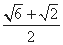

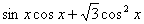 .
.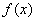 的周期;(Ⅱ)若
的周期;(Ⅱ)若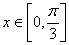 ,求函数
,求函数 的值域;
的值域;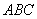 的三边
的三边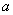 、
、 、
、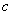 满足
满足 ,且边
,且边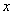 ,试求
,试求 的范围.
的范围.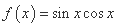 ; ②
; ②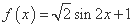 ;
;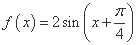 ; ④
; ④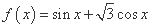 .
.
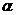 为第三象限的角,
为第三象限的角, ,则
,则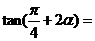
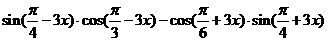 =____________.
=____________.