Question

13．已知长方体ABCD-A₁B₁C₁D₁中，M为DD₁的中点，N在AC上，且AN：NC=2：1，E为BM的中点．求证：A₁，E，N三点共线．

Answer 1

分析 以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，利用向量法能证明A₁，E，N三点共线．

解答 证明：以D为原点，DA为x轴，DC为y轴，DD₁为z轴，
建立空间直角坐标系，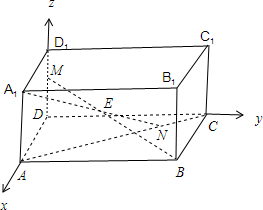
设AD=a，AB=2，AA₁=c，
则A（a，0，0），N（$\frac{1}{3}a$，$\frac{2}{3}b$，0），B（a．b.0），M（0，0，$\frac{1}{2}c$），
E（$\frac{1}{2}a$，$\frac{1}{2}b$，$\frac{1}{4}c$），A₁（a，0，c），
∴$\overrightarrow{{A}_{1}E}$=（-$\frac{1}{2}a$，$\frac{1}{2}b$，-$\frac{3}{4}c$），$\overrightarrow{{A}_{1}N}$=（-$\frac{2}{3}a$，$\frac{2}{3}b$，-c），
∴$\overrightarrow{{A}_{1}E}$=$\frac{3}{4}\overrightarrow{{A}_{1}N}$，
∵$\overrightarrow{{A}_{1}E}$与$\overrightarrow{{A}_{1}N}$有公共点A₁，
∴A₁，E，N三点共线．

点评 本题考查三点共线的证明，是基础题，解题时要认真审题，注意向量法的合理运用．