题目内容
在Rt△ABO中,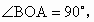
 点P为它的内切圆C上任一点,求点P到顶点A、B、O的距离的平方和的最大和最小值.
点P为它的内切圆C上任一点,求点P到顶点A、B、O的距离的平方和的最大和最小值.
答案:最大值88,最小值72
解析:
解析:
|
解:以 O为坐标原点,OA所在直线为x轴,OB所在的直线为y轴建立平面直角坐标系,如图所示.
则 A(8,0),B(0,6),设△ABO的内切圆半径为r,则
易知,此时圆心 C的坐标为C(2,2).∴△ ABO的内切圆的方程为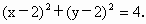
设 P(x,y)为圆上任一点,点P到顶点A、B、O的距离的平方和为d,则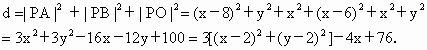
∵点 P(x,y)在圆上,∴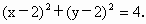 ∴ ∴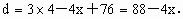
∵点 P(x,y)是圆C上的任意点,∴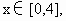
∴当 x=0时,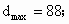 当x=4时, 当x=4时,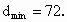
求解最值问题时,应根据条件确定出它的函数关系 (选择好自变量是顺利地解决问题的关键).本题可求出三角形ABO的内切圆的方程,根据点P在所求的圆上,变成了一个条件最值问题来求解. |

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目



 点P为它的内切圆C上任一点,求点P到顶点A、B、O的距离的平方和的最大和最小值.
点P为它的内切圆C上任一点,求点P到顶点A、B、O的距离的平方和的最大和最小值.