题目内容
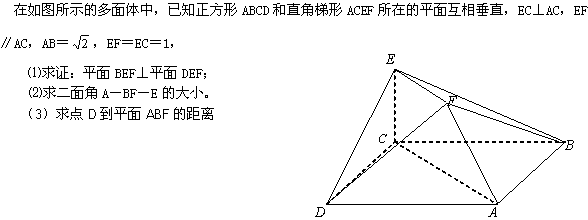
解析:⑴ ①证明: ∵平面ACEF⊥平面ABCD,EC⊥AC,
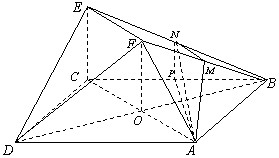 ∴EC⊥平面ABCD;连接BD交AC于点O,连接FO,
∴EC⊥平面ABCD;连接BD交AC于点O,连接FO,
∵正方形ABCD的边长为![]() ,∴AC=BD=2;
,∴AC=BD=2;
在直角梯形ACEF中,∵EF=EC=1,O为AC中点,
∴FO∥EC,且FO=1;易求得DF=BF=![]() ,
,
DE=BE=![]() ,由勾股定理知 DF⊥EF,BF⊥EF,
,由勾股定理知 DF⊥EF,BF⊥EF,
∴∠BFD是二面角B-EF-D的平面角,
由BF=DF=![]() ,BD=2可知∠BFD=
,BD=2可知∠BFD=![]() ,
,
∴平面BEF⊥平面DEF
⑵取BF中点M,BE中点N,连接AM、MN、AN,∵AB=BF=AF=![]() ,∴AM⊥BF,
,∴AM⊥BF,
又∵MN∥EF,EF⊥BF,∴MN⊥BF,∴∠AMN就是二面角A-BF-E的平面角。
易求得![]() ,
,![]() ;
;
在Rt△![]() 中,可求得
中,可求得![]() ,
,
∴在△![]() 中,由余弦定理求得
中,由余弦定理求得![]() ,
,
∴![]() ,
,
(3)等体积法:
设D点到平面ABF的距离为d 因为![]() 是正三角形且边长为
是正三角形且边长为![]()
所以![]()
![]() ,
, ![]()
![]()
所以![]() ,
, ![]() 解得d=
解得d=![]()
(或先求点O到平面ABF的距离,由D点到平面ABF的距离是O点到平面ABF距离的两倍求得)
求法:取AB的中点M连OM,FM在![]() 中过O点作斜边FM的垂线OH垂足为H,则OH为点O到平面ABF的距离,D到平面ABF的距离d=2OH
中过O点作斜边FM的垂线OH垂足为H,则OH为点O到平面ABF的距离,D到平面ABF的距离d=2OH
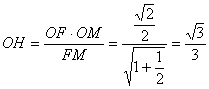 ,所以
,所以![]()

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
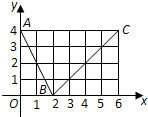 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=