题目内容
15.已知函数f(x)=$\frac{1}{2}$ax2+2x,g(x)=lnx.(1)如果函数h(x)=f(x)-g(x)在[1,+∞)上是单调减函数,求a的取值范围;
(2)是否存在实数a>0,使得方程g(x)=xf′(x)-x(2a+1)在区间($\frac{1}{e}$,e)内有解,若存在,请求出a的取值范围;若不存在,请说明理由.
(3)设r(x)=x2-ax+g($\frac{1+ax}{2}$)对于任意的a∈(1,2),总存在x0∈[$\frac{1}{2}$,1],使不等式r(x)>k(1-a2)成立,求实数k的取值范围.
分析 (1)由此利用导数性质能求出a的取值范围.
(2)由题意,原方程的根饿问题等价于方程ax2+(1-2a)x-lnx=0在($\frac{1}{e}$,e)内的零点问题,再利用导数,和零点的存在定理,求出a的范围;
(3)a∈(1,2)时,f(x)在[$\frac{1}{2}$,1]上的最大值为f(1)=ln($\frac{1}{2}$+$\frac{1}{2}$a)+1-a,于是问题等价于:对任意的a∈(1,2),不等式ln($\frac{1}{2}$+$\frac{1}{2}$a)+1-a+k(a2-1)>0恒成立,再利用导函数研究不等式左边的最小值看是否符合要求即可求实数m的取值范围.
解答 解:(1)由已知,得h(x)=$\frac{1}{2}$ax2+2x-lnx,且x>0,
则h′(x)=ax+2-$\frac{1}{x}$=$\frac{{ax}^{2}+2x-1}{x}$,
∵函数 h(x)在[1,+∞)上是减函数,
∴h′(x)≤0恒成立,
∴ax2+2x-1≤0在[1,∞)恒成立,
即a≤$\frac{1}{{x}^{2}}$-$\frac{2}{x}$=${(\frac{1}{x}-1)}^{2}$-1,(0<$\frac{1}{x}$≤1),
∴a≤-1,
即a的取值范围是 (-∞,-1];
(2)方程g(x)=xf′(x)-x(2a+1),等价于方程ax2+(1-2a)x-lnx=0,
设 H(x)=ax2+(1-2a)x-lnx,
于是原方程在区间($\frac{1}{e}$,e)内根的问题,转化为函数H(x)在($\frac{1}{e}$,e)内的零点问题.
H′(x)=2ax+(1-2a)-$\frac{1}{x}$=$\frac{(2ax+1)(x-1)}{x}$,
当 x∈(0,1)时,H'(x)<0,H(x)是减函数,
当 x∈(1,+∞)时,H'(x)>0,H(x)是增函数,
若 H(x)在($\frac{1}{e}$,e)内有零点,
只需$\left\{\begin{array}{l}{H(\frac{1}{e})=\frac{a}{{e}^{2}}+\frac{1-2a}{e}+1≥0}\\{{H}_{min}(x)=H(1)=a+(1-2a)≤0}\\{H(e)={ae}^{2}+(1-2a)e-1≥0}\end{array}\right.$,
解得:1≤a≤$\frac{{e}^{2}+e}{2e-1}$即a的取值范围是[1,$\frac{{e}^{2}+e}{2e-1}$];
(3)a∈(1,2)时,f(x)在[$\frac{1}{2}$,1]上的最大值为f(1)=ln($\frac{1}{2}$+$\frac{1}{2}$a)+1-a,
于是问题等价于:对任意的a∈(1,2),不等式ln($\frac{1}{2}$+$\frac{1}{2}$a)+1-a+k(a2-1)>0恒成立.
记g(a)=ln($\frac{1}{2}$+$\frac{1}{2}$a)+1-a+k(a2-1),(1<a<2)
则g′(a)=$\frac{a}{1+a}$[2ka-(1-2k)],
当k=0时,g′(a)=$\frac{-a}{1+a}$<0,∴g(a)在区间(1,2)上递减,此时,g(a)<g(1)=0,
由于a2-1>0,∴k≤0时不可能使g(a)>0恒成立,
故必有k>0,∴g′(a)=$\frac{a}{1+a}$[2ka-(1-2k)].
若$\frac{1}{2k}$-1>1,可知g(a)在区间(1,min{2,$\frac{1}{2k}$-1})上递减,
在此区间上,有g(a)<g(1)=0,与g(a)>0恒成立矛盾,故$\frac{1}{2k}$-1≤1,
这时,g'(a)>0,g(a)在(1,2)上递增,恒有g(a)>g(1)=0,满足题设要求,
∴$\left\{\begin{array}{l}{k>0}\\{\frac{1}{2k}-1≤1}\end{array}\right.$,即k≥$\frac{1}{4}$,
∴实数k的取值范围为[$\frac{1}{4}$,+∞).
点评 本题考查利用导数研究函数单调性,考查函数恒成立问题,考查函数与方程思想、分类讨论思想,综合性强,难度大.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案| A. | $\frac{7}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{5}{4}$ |
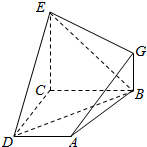 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD丄平面BCEG,BC=CD=CE=2AD=2BG=2.
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=$\frac{π}{2}$,平面ABCD丄平面BCEG,BC=CD=CE=2AD=2BG=2.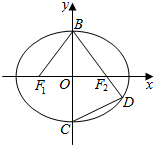 如图,在平面直角坐标系xOy中,F1,F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,B,C分别为椭圆上、下顶点,直线BF2与椭圆的另一个交点为D,若tan∠F1BO=$\frac{3}{4}$,则直线CD的斜率为$\frac{12}{25}$.
如图,在平面直角坐标系xOy中,F1,F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,B,C分别为椭圆上、下顶点,直线BF2与椭圆的另一个交点为D,若tan∠F1BO=$\frac{3}{4}$,则直线CD的斜率为$\frac{12}{25}$.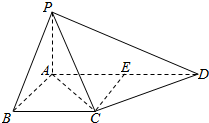 如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.
如图,在梯形ABCD中,AD∥BC,AB⊥BC,AB=BC=1,PA⊥平面ABCD,CD⊥PC,PD=2PA.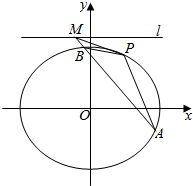 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,3),离心率e=$\frac{1}{2}$,直线1的方程为y=4.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,3),离心率e=$\frac{1}{2}$,直线1的方程为y=4.