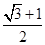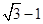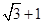题目内容
已知中心在原点,焦点在 轴上的双曲线的离心率为
轴上的双曲线的离心率为 ,则它的渐近线方程为( )
,则它的渐近线方程为( )
A. | B. | C.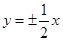 | D. |
D
解析试题分析:因为双曲线焦点在y轴上,由双曲线a,b,c,e的关系得, ,解得
,解得 =
= ,所以它的渐近线方程为
,所以它的渐近线方程为 ,故选D。
,故选D。
考点:本题主要考查双曲线的几何性质。
点评:基础题,作为选择题,可以利用结合选项代人验证。

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
若双曲线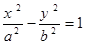 与椭圆
与椭圆 (m>b>0 )的离心率之积大于1,则以
(m>b>0 )的离心率之积大于1,则以 为边长的三角形一定是( )
为边长的三角形一定是( )
| A.等腰三角形 | B.直角三角形 | C.锐角三角形 | D.钝角三角形 |
已知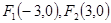 ,动点
,动点 满足:
满足: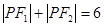 ,则动点
,则动点 的轨迹为( )
的轨迹为( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.线段 |
已知双曲线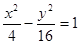 的渐近线
的渐近线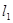 经过二、四象,直线
经过二、四象,直线 过点
过点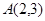 且垂直于直线
且垂直于直线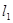 ,则直线
,则直线 方程为( )
方程为( )
A.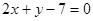 | B.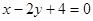 |
C.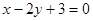 | D.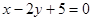 |
抛物线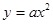 的焦点坐标为
的焦点坐标为
A.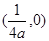 | B.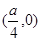 | C. | D.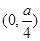 |
已知已知点(2,3)在双曲线C: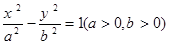 上,C的焦距为4,
上,C的焦距为4,
则它的离心率为( )
| A.2 | B.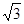 | C.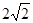 | D. |
直线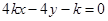 与抛物线
与抛物线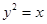 交于
交于 、
、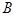 两点,若
两点,若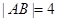 ,则弦
,则弦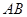 的中点到直线
的中点到直线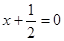 的距离等于( )
的距离等于( )
A.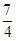 | B.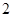 | C. | D.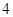 |
 、
、 是一对相关曲线的焦点,
是一对相关曲线的焦点, 是它们在第一象限的交点,当
是它们在第一象限的交点,当 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( )
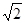

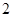
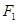 和
和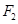 分别是双曲线
分别是双曲线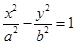 (
(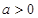 ,
,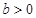 )的两个焦点,A和B是以O为圆心,以
)的两个焦点,A和B是以O为圆心,以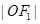 为半径的圆与该双曲线左支的两个交点,且
为半径的圆与该双曲线左支的两个交点,且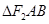 是等边三角形,则该双曲线的离心率为
是等边三角形,则该双曲线的离心率为