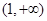题目内容
我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知 、
、 是一对相关曲线的焦点,
是一对相关曲线的焦点, 是它们在第一象限的交点,当
是它们在第一象限的交点,当 时,这一对相关曲线中双曲线的离心率是( )
时,这一对相关曲线中双曲线的离心率是( )
A. | B.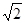 | C. | D.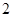 |
A
解析试题分析:记F1P=m,F2P=n,F1F2=2c,由余弦定理得(2c)2=m2+n2-2mncos600,即4c2=m2+n2-mn。
设a1是椭圆的长半轴,a2是双曲线的实半轴,由椭圆及双曲线定义,得m+n=2a1,m-n=2a2,即m=a1+a2,n=a1-a2,将它们及离心率互为倒数关系代入前式得a12-4a1a2+a22=0,可求得a1=3a2,e1×e2=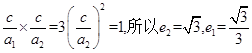 。所以这一对相关曲线中双曲线的离心率是
。所以这一对相关曲线中双曲线的离心率是 。
。
考点:椭圆的简单性质;双曲线的简单性质;余弦定理。
点评:本题考查圆锥曲线的共同特征,考查了椭圆与双曲线的性质,解题的关键是理解定义,且灵活应用定义。本题考查了阅读能力及推理判断的能力,本部分题符号计算多,运算量大,解题时要认真严谨,避免马虎出错。

练习册系列答案
相关题目
已知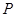 是以
是以 为焦点的椭圆
为焦点的椭圆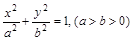 上的一点,若
上的一点,若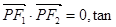
 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A. | B.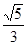 | C.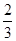 | D.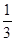 |
已知中心在原点,焦点在 轴上的双曲线的离心率为
轴上的双曲线的离心率为 ,则它的渐近线方程为( )
,则它的渐近线方程为( )
A. | B. | C.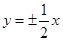 | D. |
设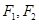 是椭圆
是椭圆 的两个焦点,点M在椭圆上,若△
的两个焦点,点M在椭圆上,若△ 是直角三角形,则△
是直角三角形,则△ 的面积等于( )
的面积等于( )
| A.48/5 | B.36/5 | C.16 | D.48/5或16 |
抛物线 的焦点坐标是( )
的焦点坐标是( )
| A.(2,0) | B.(- 2,0) | C.(4,0) | D.(- 4,0) |
若抛物线y2=2px的焦点与椭圆 的右焦点重合,则p的值为( )
的右焦点重合,则p的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
 (
( ,
, )的左、右焦点分别是
)的左、右焦点分别是 ,过
,过 作倾斜角为
作倾斜角为 的直线交双曲线右支于
的直线交双曲线右支于 点,若
点,若 垂直于
垂直于 轴,则双曲线的离心率为
轴,则双曲线的离心率为


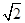
 分别是双曲线
分别是双曲线 的左,右焦点,若在双曲线右支上存在点P,满足
的左,右焦点,若在双曲线右支上存在点P,满足 ,且
,且 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的离心率等于( )
的距离等于双曲线的实轴长,则该双曲线的离心率等于( )


 分别为双曲线
分别为双曲线 的左、右焦点,
的左、右焦点, 为双曲线左支上的一点,若
为双曲线左支上的一点,若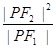 的值为
的值为 ,则双曲线离心率的取值范围是( )
,则双曲线离心率的取值范围是( )