题目内容
已知F1、F2是椭圆x2+
=1的两个焦点,AB是过焦点F1的一条动弦,求△ABF2的面积的最大值.
| y2 |
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:当AB与椭圆长轴垂直时,△ABF2的面积取最大值,由此能求出结果.
解答:
解:∵F1、F2是椭圆x2+
=1的两个焦点,
∴F1(0,-1),a=
,b=c=1,
∵AB是过焦点F1的一条动弦,
∴将直线AB绕F1点旋转,
根据椭圆的几何性质,得:
当AB与椭圆长轴垂直时,△ABF2的面积取最大值,
∴△ABF2的面积的最大值S=
×
×2c=
×
×2=
.
∴△ABF2的面积的最大值是
.
| y2 |
| 2 |
∴F1(0,-1),a=
| 2 |
∵AB是过焦点F1的一条动弦,
∴将直线AB绕F1点旋转,
根据椭圆的几何性质,得:
当AB与椭圆长轴垂直时,△ABF2的面积取最大值,
∴△ABF2的面积的最大值S=
| 1 |
| 2 |
| 2b2 |
| a |
| 1 |
| 2 |
| 2 | ||
|
| 2 |
∴△ABF2的面积的最大值是
| 2 |
点评:本题考查三角形面积的最大值的求法,是中档题,解题时要认真审题,注意椭圆性质的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=x+sinx,x∈[-π,π]的大致图象是( )
A、 |
B、 |
C、 |
D、 |
 如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=1,BC=
如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=1,BC=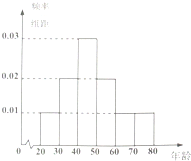 “行通济”是广东佛山一带在元宵节期间举行的游玩祈福活动,每到这一天,家家户户都会扶老携幼,自清晨到夜幕,举着风车、摇着风铃、拎着生菜浩浩荡荡地由北到南走过通济桥,祈求来年平平安安、顺顺利利.为了了解不同年龄层次的人对这一传统习俗的参与度,现随机抽取年龄在20~80岁之间的60人,并按年龄层次[20,30),[30,40),[40,50),[50,60),[60,70),[70,80)绘制频率分布直方图如图所示,其中参与了2014年“行通济”活动的人数如下表.若规定年龄分布在[20,60)岁的为“中青年人”,60岁以上(含60岁)为“老年人”.
“行通济”是广东佛山一带在元宵节期间举行的游玩祈福活动,每到这一天,家家户户都会扶老携幼,自清晨到夜幕,举着风车、摇着风铃、拎着生菜浩浩荡荡地由北到南走过通济桥,祈求来年平平安安、顺顺利利.为了了解不同年龄层次的人对这一传统习俗的参与度,现随机抽取年龄在20~80岁之间的60人,并按年龄层次[20,30),[30,40),[40,50),[50,60),[60,70),[70,80)绘制频率分布直方图如图所示,其中参与了2014年“行通济”活动的人数如下表.若规定年龄分布在[20,60)岁的为“中青年人”,60岁以上(含60岁)为“老年人”.