题目内容
11．已知α为第四象限的角，且cos（$\frac{π}{2}$+α）=$\frac{4}{5}$，则tanα=-$\frac{4}{3}$．分析 由条件利用同角三角函数的基本关系，求得tanα的值．
解答 解：∵α为第四象限的角，且cos（$\frac{π}{2}$+α）=-sinsα=$\frac{4}{5}$，∴sinα=-$\frac{4}{5}$，cosα=$\sqrt{{1-sin}^{2}α}$=$\frac{3}{5}$，
则tanα=$\frac{sinα}{cosα}$=-$\frac{4}{3}$，
故答案为：$-\frac{4}{3}$．
点评 本题主要考查同角三角函数的基本关系的应用，属于基础题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
1．
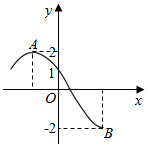如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤$\frac{π}{2}$）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）
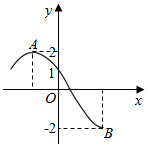如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤$\frac{π}{2}$）的部分图象，其中A，B两点之间的距离为5，那么f（-1）=（ ）| A． | -1 | B． | -$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | 1 |
20．若（1-$\frac{2}{x}$）2n的展开式有9项，则n的值为．
| A． | 5 | B． | 4 | C． | 9 | D． | $\frac{9}{4}$ |
6．已知|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=$\sqrt{3}$，$\overrightarrow{a}$+$\overrightarrow{b}$=（$\sqrt{3}$，1），则$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |