题目内容
已知椭圆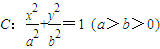 经过点A(2,1),离心率为
经过点A(2,1),离心率为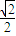 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)过点(3,0)的直线l与椭圆C交于不同的两点M,N,设直线AM和直线AN的斜率分别为kAM和kAN,求证:kAM+kAN为定值.
【答案】分析:(Ⅰ)由题意得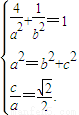 ,由此能求出椭圆C的方程中参数a,b的值.
,由此能求出椭圆C的方程中参数a,b的值.
(Ⅱ)由题意可设直线l方程为y=k(x-3),由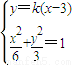 得(1+2k2)x2-12k2x+18k2-6=0.因为直线l与椭圆C交于不同的两点M,N,所以△=144k4-4(1+2k2)(18k2-6)=24(1-k2)>0,解得-1<k<1.由此入手能够证明kAM+kAN为定值.
得(1+2k2)x2-12k2x+18k2-6=0.因为直线l与椭圆C交于不同的两点M,N,所以△=144k4-4(1+2k2)(18k2-6)=24(1-k2)>0,解得-1<k<1.由此入手能够证明kAM+kAN为定值.
解答:解:(Ⅰ)由题意得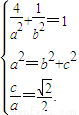 (2分)
(2分)
解得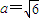 ,
,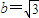 . (4分)
. (4分)
故椭圆C的方程为 . (5分)
. (5分)
(Ⅱ)由题意可设直线l方程为y=k(x-3),
由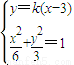 得(1+2k2)x2-12k2x+18k2-6=0.(7分)
得(1+2k2)x2-12k2x+18k2-6=0.(7分)
因为直线l与椭圆C交于不同的两点M,N,
所以△=144k4-4(1+2k2)(18k2-6)=24(1-k2)>0,解得-1<k<1.…(8分)
设M,N的坐标分别为(x1,y1),(x2,y2),
则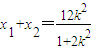 ,
,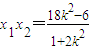 ,(10分)
,(10分)
y1=k(x1-3),y2=k(x2-3).
所以kAM+kAN= (12分)
(12分)
=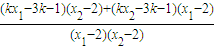
=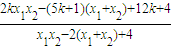
=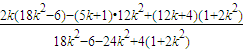
=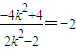 .
.
所以kAM+kAN为定值-2. (14分)
点评:本题考查椭圆方程的求法和证明kAM+kAN为定值.解题时要认真审题,仔细解答,注意合理地进行等价转化.
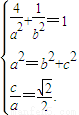 ,由此能求出椭圆C的方程中参数a,b的值.
,由此能求出椭圆C的方程中参数a,b的值.(Ⅱ)由题意可设直线l方程为y=k(x-3),由
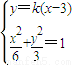 得(1+2k2)x2-12k2x+18k2-6=0.因为直线l与椭圆C交于不同的两点M,N,所以△=144k4-4(1+2k2)(18k2-6)=24(1-k2)>0,解得-1<k<1.由此入手能够证明kAM+kAN为定值.
得(1+2k2)x2-12k2x+18k2-6=0.因为直线l与椭圆C交于不同的两点M,N,所以△=144k4-4(1+2k2)(18k2-6)=24(1-k2)>0,解得-1<k<1.由此入手能够证明kAM+kAN为定值.解答:解:(Ⅰ)由题意得
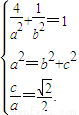 (2分)
(2分)解得
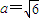 ,
,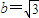 . (4分)
. (4分)故椭圆C的方程为
 . (5分)
. (5分)(Ⅱ)由题意可设直线l方程为y=k(x-3),
由
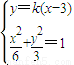 得(1+2k2)x2-12k2x+18k2-6=0.(7分)
得(1+2k2)x2-12k2x+18k2-6=0.(7分)因为直线l与椭圆C交于不同的两点M,N,
所以△=144k4-4(1+2k2)(18k2-6)=24(1-k2)>0,解得-1<k<1.…(8分)
设M,N的坐标分别为(x1,y1),(x2,y2),
则
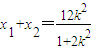 ,
,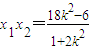 ,(10分)
,(10分)y1=k(x1-3),y2=k(x2-3).
所以kAM+kAN=
 (12分)
(12分)=
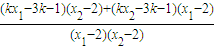
=
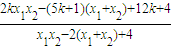
=
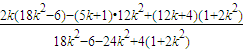
=
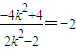 .
.所以kAM+kAN为定值-2. (14分)
点评:本题考查椭圆方程的求法和证明kAM+kAN为定值.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 经过点A(2,1),离心率为
经过点A(2,1),离心率为 ,过点B(3,0)的直线l与椭圆交于不同的两点M,N.
,过点B(3,0)的直线l与椭圆交于不同的两点M,N. 的取值范围.
的取值范围.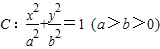 经过点A(2,1),离心率为
经过点A(2,1),离心率为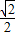 .过点B(3,0)的直线l与椭圆C交于不同的两点M,N.
.过点B(3,0)的直线l与椭圆C交于不同的两点M,N. 的取值范围;
的取值范围; 经过点A(2,1),离心率为
经过点A(2,1),离心率为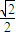 ,过点B(3,0)的直线l与椭圆交于不同的两点M,N.
,过点B(3,0)的直线l与椭圆交于不同的两点M,N.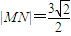 ,求直线MN的方程.
,求直线MN的方程.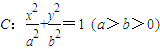 经过点A(2,1),离心率为
经过点A(2,1),离心率为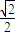 .过点B(3,0)的直线l与椭圆C交于不同的两点M,N.
.过点B(3,0)的直线l与椭圆C交于不同的两点M,N.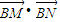 的取值范围;
的取值范围;