题目内容
已知椭圆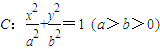 经过点A(2,1),离心率为
经过点A(2,1),离心率为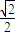 .过点B(3,0)的直线l与椭圆C交于不同的两点M,N.
.过点B(3,0)的直线l与椭圆C交于不同的两点M,N.(Ⅰ)求椭圆C的方程;
(Ⅱ)求
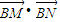 的取值范围;
的取值范围;(Ⅲ)设直线AM和直线AN的斜率分别为kAM和kAN,求证:kAM+kAN为定值.
【答案】分析:(Ⅰ)根据离心率和(2,1)点代入椭圆方程可求得a和c,进而求得b,方程可得.
(Ⅱ)由题意显然直线l的斜率存在,设直线l方程为y=k(x-3),联立直线与椭圆的方程 ,消去y得(1+2k2)x2-12k2x+18k2-6=0.因为直线l与椭圆C交于不同的两点M,N,所以△>0,可得-1<k<1.再用坐标表示出
,消去y得(1+2k2)x2-12k2x+18k2-6=0.因为直线l与椭圆C交于不同的两点M,N,所以△>0,可得-1<k<1.再用坐标表示出 即可求
即可求 的取值范围.
的取值范围.
(Ⅲ)由(Ⅱ)用坐标表示出kAM+kAN化简即可.
解答:解:(Ⅰ)由题意得 ,解得
,解得 ,
, .故椭圆C的方程为
.故椭圆C的方程为 .
.
(Ⅱ)由题意显然直线l的斜率存在,设直线l方程为y=k(x-3),
由 得(1+2k2)x2-12k2x+18k2-6=0.
得(1+2k2)x2-12k2x+18k2-6=0.
因为直线l与椭圆C交于不同的两点M,N,所以△=144k4-4(1+2k2)(18k2-6)=24(1-k2)>0,解得-1<k<1.
设M,N的坐标分别为(x1,y1),(x2,y2),则 ,
, ,
,
y1=k(x1-3),y2=k(x2-3).
所以
=(1+k2)[x1x2-3(x1+x2)+9]= =
= .
.
因为-1<k<1,所以 .
.
故 的取值范围为(2,3].
的取值范围为(2,3].
(Ⅲ)由(Ⅱ)得kAM+kAN=
= =
=
= =
= .
.
所以kAM+kAN为定值-2.
点评:本题主要考查了椭圆方程的求解,考查直线与椭圆的位置关系,利用直线与椭圆方程联立,借助于根与系数的关系,从而使问题得解.
(Ⅱ)由题意显然直线l的斜率存在,设直线l方程为y=k(x-3),联立直线与椭圆的方程
 ,消去y得(1+2k2)x2-12k2x+18k2-6=0.因为直线l与椭圆C交于不同的两点M,N,所以△>0,可得-1<k<1.再用坐标表示出
,消去y得(1+2k2)x2-12k2x+18k2-6=0.因为直线l与椭圆C交于不同的两点M,N,所以△>0,可得-1<k<1.再用坐标表示出 即可求
即可求 的取值范围.
的取值范围.(Ⅲ)由(Ⅱ)用坐标表示出kAM+kAN化简即可.
解答:解:(Ⅰ)由题意得
 ,解得
,解得 ,
, .故椭圆C的方程为
.故椭圆C的方程为 .
.(Ⅱ)由题意显然直线l的斜率存在,设直线l方程为y=k(x-3),
由
 得(1+2k2)x2-12k2x+18k2-6=0.
得(1+2k2)x2-12k2x+18k2-6=0.因为直线l与椭圆C交于不同的两点M,N,所以△=144k4-4(1+2k2)(18k2-6)=24(1-k2)>0,解得-1<k<1.
设M,N的坐标分别为(x1,y1),(x2,y2),则
 ,
, ,
,y1=k(x1-3),y2=k(x2-3).
所以

=(1+k2)[x1x2-3(x1+x2)+9]=
 =
= .
.因为-1<k<1,所以
 .
.故
 的取值范围为(2,3].
的取值范围为(2,3].(Ⅲ)由(Ⅱ)得kAM+kAN=

=
 =
=
=
 =
= .
.所以kAM+kAN为定值-2.
点评:本题主要考查了椭圆方程的求解,考查直线与椭圆的位置关系,利用直线与椭圆方程联立,借助于根与系数的关系,从而使问题得解.

练习册系列答案
相关题目
 经过点A(2,1),离心率为
经过点A(2,1),离心率为 ,过点B(3,0)的直线l与椭圆交于不同的两点M,N.
,过点B(3,0)的直线l与椭圆交于不同的两点M,N. 的取值范围.
的取值范围.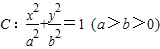 经过点A(2,1),离心率为
经过点A(2,1),离心率为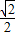 .过点B(3,0)的直线l与椭圆C交于不同的两点M,N.
.过点B(3,0)的直线l与椭圆C交于不同的两点M,N. 的取值范围;
的取值范围; 经过点A(2,1),离心率为
经过点A(2,1),离心率为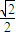 ,过点B(3,0)的直线l与椭圆交于不同的两点M,N.
,过点B(3,0)的直线l与椭圆交于不同的两点M,N.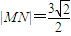 ,求直线MN的方程.
,求直线MN的方程.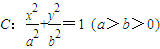 经过点A(2,1),离心率为
经过点A(2,1),离心率为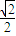 .
.