题目内容
将函数y=sin（2x+φ）的图象沿x轴向左平移
个单位后，得到一个关于y轴对称的图象，则φ的一个可能取值为（ ）
| π |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的求值,三角函数的图像与性质
分析：首先对函数进行平移变换，再利用对称性求解．
解答：
解：函数y=sin（2x+φ）的图象沿x轴向左平移
个单位后，
得到：f(x)=sin(2x+
+φ)由于函数图象关于y轴对称，
所以
+φ=kπ+
（k∈Z）
当k=0时，φ=
故选：C
| π |
| 8 |
得到：f(x)=sin(2x+
| π |
| 4 |
所以
| π |
| 4 |
| π |
| 2 |
当k=0时，φ=
| π |
| 4 |
故选：C
点评：本题考查的知识要点：三角函数的平移变换问题，函数的对称问题，诱导公式的灵活应用．
练习册系列答案
相关题目
若x、y满足约束条件
目标函数z=ax+2y仅在点（1，0）处取得最小值，则a的取值范围是（ ）
|
| A、（-4，2） |
| B、（-1，2） |
| C、（-4，0） |
| D、（-2，4） |
设函数f（x）的零点为x1，g（x）=4x+2x-2的零点为x2，若|x1-x2|≤0.25，则f（x）可以是（ ）
| A、f（x）=（x-1）2 | ||
| B、f（x）=ex-1 | ||
C、f(x)=ln(x-
| ||
| D、f（x）=4x-1 |
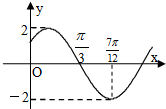如图是函数y=Asin（ωx+φ）（A＞0，ω＞0）的部分图象，则下列可以作为其解析式的是（ ）A、y=2sin（2x-
| ||||
B、y=2sin（
| ||||
C、y=2sin（2x-
| ||||
D、y=2sin（2x+
|
已知命题p：?x∈R，2x＞0；命题q：在曲线y=cosx上存在斜率为
的切线，则下列判断正确的是（ ）
| 2 |
| A、p是假命题 |
| B、q是真命题 |
| C、p∧（￢q）是真命题 |
| D、（￢p）∧q是真命题 |
在数列{xn}中，
=
+
（n≥2），且x2=
，x4=
，则x10等于（ ）
| 2 |
| xn |
| 1 |
| xn-1 |
| 1 |
| xn+1 |
| 2 |
| 3 |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|