题目内容
已知向量 ,当x>0时,定义函数
,当x>0时,定义函数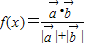 .
.(1)求函数y=f(x)的反函数y=f-1(x);
(2)数列{an}满足:a1=a>0,an+1=f(an),n∈N*,Sn为数列{an}的前n项和,则:
①当a=1时,证明:
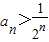 ;
;②对任意θ∈[0,2π],当2asinθ-2a+Sn≠0时,
证明:
 或
或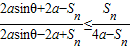 .
.
【答案】分析:(1)由题意得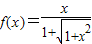 ,令x=tanα
,令x=tanα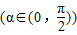 ,则
,则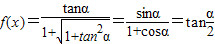 ,函数f(x)的值域为(0,1).由此能求出原函数的反函数.
,函数f(x)的值域为(0,1).由此能求出原函数的反函数.
(2)因为a1=a>0,an+1=f(an),n∈N*,所以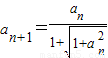 .
.
①【法一】三角代换:令an=tanαn,因为an>0,且a1=1所以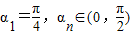 ,所以
,所以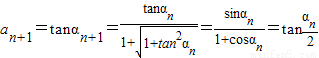 ,由此能够证明
,由此能够证明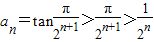 .
.
【法二】不等式放缩:因为an+1=f(an),所以an=f-1(an+1),故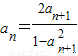 ,又由原函数的值域知an+1∈(0,1),所以
,又由原函数的值域知an+1∈(0,1),所以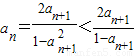 ,则
,则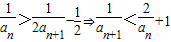 ,由此能够证明
,由此能够证明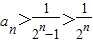 .
.
②【法一】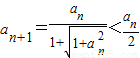 ,所以
,所以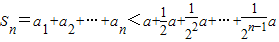 =
=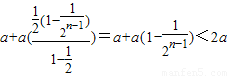 .由Sn<2a,能够证明证明
.由Sn<2a,能够证明证明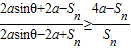 或
或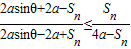 .
.
【法二】因为an+1=f(an),所以an=f-1(an+1),所以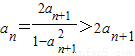 ,从而
,从而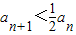 .由Sn<2a,能够证明证明
.由Sn<2a,能够证明证明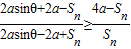 或
或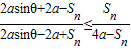 .
.
解答:解:由题意得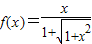 (x>0)
(x>0)
令x=tanα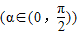 ,则
,则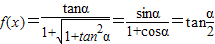
由于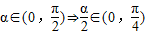 ,所以
,所以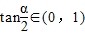 ,即函数f(x)的值域为(0,1)
,即函数f(x)的值域为(0,1)
(1)由 y2-2xy+x2=y2+y2x2
y2-2xy+x2=y2+y2x2
于是解得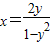 ,所以原函数的反函数
,所以原函数的反函数 (0<x<1)
(0<x<1)
(2)因为a1=a>0,an+1=f(an),n∈N*,所以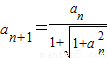
①【法一】三角代换 令an=tanαn,因为an>0,且a1=1所以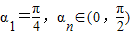
所以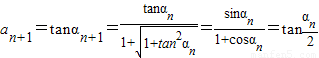
由于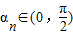 ,所以
,所以
故数列{αn}为等比数列,其首项为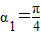 ,公比为
,公比为 ,所以
,所以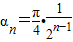
于是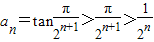 ,此处用到不等式x<tanx
,此处用到不等式x<tanx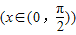
【法二】不等式放缩 因为an+1=f(an),所以an=f-1(an+1)
所以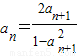 ,又由原函数的值域知an+1∈(0,1)
,又由原函数的值域知an+1∈(0,1)
所以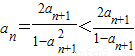 ,则
,则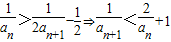
进而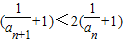 ,所以
,所以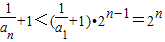 于是
于是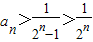
②【法一】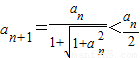 ,所以
,所以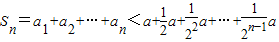 =
=
由Sn<2a,则易得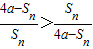 ,又Sn>0
,又Sn>0
则要证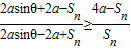 或
或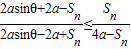
等价于证明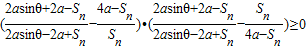
化简等价于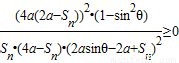 ,此式在0<Sn<2a的条件下成立;
,此式在0<Sn<2a的条件下成立;
【法二】因为an+1=f(an),所以an=f-1(an+1)
所以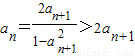 ,从而
,从而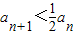 从而Sn<2a.
从而Sn<2a.
则易得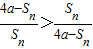 ,又Sn>0
,又Sn>0
则要证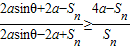 或
或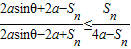
等价于证明
化简等价于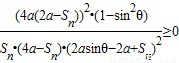 ,此式在0<Sn<2a的条件下成立;
,此式在0<Sn<2a的条件下成立;
点评:本题考查数列的综合运用,解题时要认真审题,仔细解答,合理地运用三角函数知识,注意挖掘题设中的隐含条件,合理地进行等价转化.
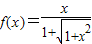 ,令x=tanα
,令x=tanα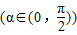 ,则
,则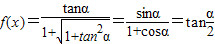 ,函数f(x)的值域为(0,1).由此能求出原函数的反函数.
,函数f(x)的值域为(0,1).由此能求出原函数的反函数.(2)因为a1=a>0,an+1=f(an),n∈N*,所以
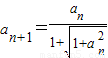 .
.①【法一】三角代换:令an=tanαn,因为an>0,且a1=1所以
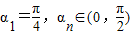 ,所以
,所以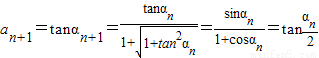 ,由此能够证明
,由此能够证明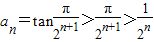 .
.【法二】不等式放缩:因为an+1=f(an),所以an=f-1(an+1),故
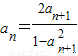 ,又由原函数的值域知an+1∈(0,1),所以
,又由原函数的值域知an+1∈(0,1),所以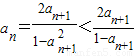 ,则
,则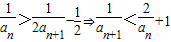 ,由此能够证明
,由此能够证明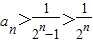 .
.②【法一】
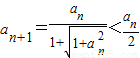 ,所以
,所以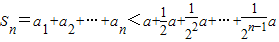 =
=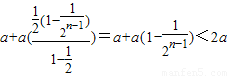 .由Sn<2a,能够证明证明
.由Sn<2a,能够证明证明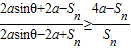 或
或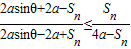 .
.【法二】因为an+1=f(an),所以an=f-1(an+1),所以
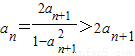 ,从而
,从而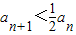 .由Sn<2a,能够证明证明
.由Sn<2a,能够证明证明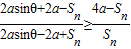 或
或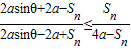 .
.解答:解:由题意得
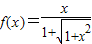 (x>0)
(x>0)令x=tanα
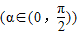 ,则
,则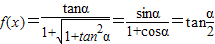
由于
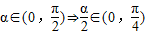 ,所以
,所以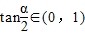 ,即函数f(x)的值域为(0,1)
,即函数f(x)的值域为(0,1)(1)由
 y2-2xy+x2=y2+y2x2
y2-2xy+x2=y2+y2x2于是解得
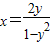 ,所以原函数的反函数
,所以原函数的反函数 (0<x<1)
(0<x<1)(2)因为a1=a>0,an+1=f(an),n∈N*,所以
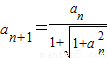
①【法一】三角代换 令an=tanαn,因为an>0,且a1=1所以
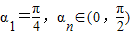
所以
由于
 ,所以
,所以
故数列{αn}为等比数列,其首项为
 ,公比为
,公比为 ,所以
,所以
于是
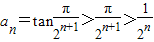 ,此处用到不等式x<tanx
,此处用到不等式x<tanx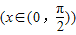
【法二】不等式放缩 因为an+1=f(an),所以an=f-1(an+1)
所以
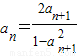 ,又由原函数的值域知an+1∈(0,1)
,又由原函数的值域知an+1∈(0,1)所以
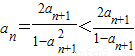 ,则
,则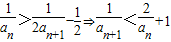
进而
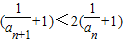 ,所以
,所以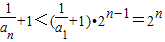 于是
于是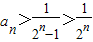
②【法一】
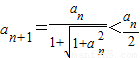 ,所以
,所以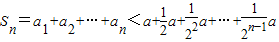 =
=
由Sn<2a,则易得
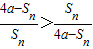 ,又Sn>0
,又Sn>0则要证
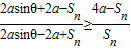 或
或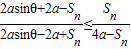
等价于证明
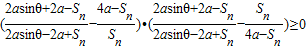
化简等价于
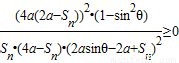 ,此式在0<Sn<2a的条件下成立;
,此式在0<Sn<2a的条件下成立;【法二】因为an+1=f(an),所以an=f-1(an+1)
所以
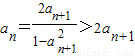 ,从而
,从而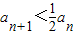 从而Sn<2a.
从而Sn<2a.则易得
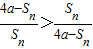 ,又Sn>0
,又Sn>0则要证
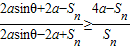 或
或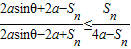
等价于证明

化简等价于
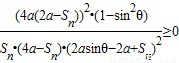 ,此式在0<Sn<2a的条件下成立;
,此式在0<Sn<2a的条件下成立;点评:本题考查数列的综合运用,解题时要认真审题,仔细解答,合理地运用三角函数知识,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
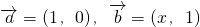 ,当x>0时,定义函数
,当x>0时,定义函数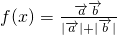 .
.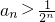 ;
;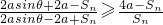 或
或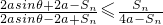 .
.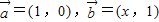 ,当x>0时,定义函数
,当x>0时,定义函数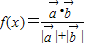 .
.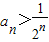 .
.