题目内容
已知向量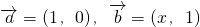 ,当x>0时,定义函数
,当x>0时,定义函数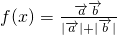 .
.
(1)求函数y=f(x)的反函数y=f-1(x);
(2)数列{an}满足:a1=a>0,an+1=f(an),n∈N*,Sn为数列{an}的前n项和,
①证明:Sn<2a;
②当a=1时,证明: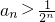 .
.
解:由题意得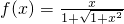 (x>0)
(x>0)
令x=tanα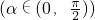 ,则
,则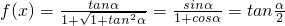
由于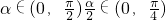 ,所以
,所以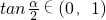 ,即函数f(x)的值域为(0,1)
,即函数f(x)的值域为(0,1)
(1)由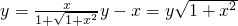 y2-2xy+x2=y2+y2x2
y2-2xy+x2=y2+y2x2
于是解得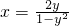 ,所以原函数的反函数
,所以原函数的反函数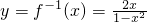 (0<x<1)
(0<x<1)
(2)证明:因为a1=a>0,an+1=f(an),n∈N*,所以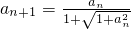
∴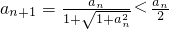 ,所以
,所以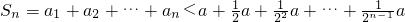 =
=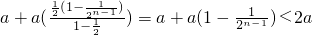
②因为an+1=f(an),所以an=f-1(an+1)
所以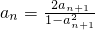 ,又由原函数的值域知an+1∈(0,1)
,又由原函数的值域知an+1∈(0,1)
所以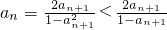 ,则
,则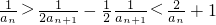
进而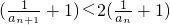 ,所以
,所以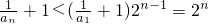
于是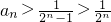
分析:由题意得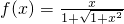 (x>0),令x=tanα
(x>0),令x=tanα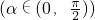 ,则
,则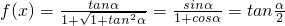 ,由于
,由于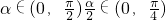 ,所以
,所以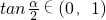 ,即函数f(x)的值域为(0,1)
,即函数f(x)的值域为(0,1)
(1)由 ,反解x可得
,反解x可得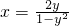 ,所以原函数的反函数
,所以原函数的反函数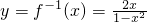 (0<x<1)
(0<x<1)
(2)因为a1=a>0,an+1=f(an),n∈N*,所以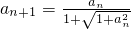
①利用放缩法.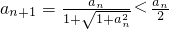 ,所以
,所以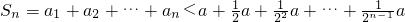 =
=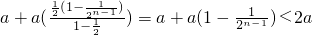
②因为an+1=f(an),所以an=f-1(an+1),所以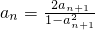 ,又由原函数的值域知an+1∈(0,1),所以
,又由原函数的值域知an+1∈(0,1),所以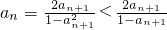 ,则
,则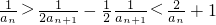 ,进而
,进而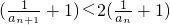 ,所以
,所以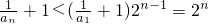 于是可得结论.
于是可得结论.
点评:本题以新定义为载体,考查函数及反函数的求解,考查不等式的证明,解题的关键是适当放缩,难度较大.
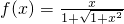 (x>0)
(x>0)令x=tanα
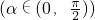 ,则
,则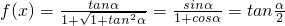
由于
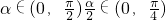 ,所以
,所以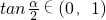 ,即函数f(x)的值域为(0,1)
,即函数f(x)的值域为(0,1)(1)由
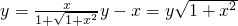 y2-2xy+x2=y2+y2x2
y2-2xy+x2=y2+y2x2于是解得
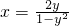 ,所以原函数的反函数
,所以原函数的反函数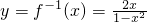 (0<x<1)
(0<x<1)(2)证明:因为a1=a>0,an+1=f(an),n∈N*,所以
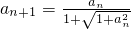
∴
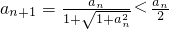 ,所以
,所以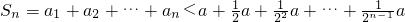 =
=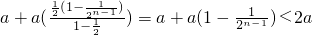
②因为an+1=f(an),所以an=f-1(an+1)
所以
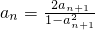 ,又由原函数的值域知an+1∈(0,1)
,又由原函数的值域知an+1∈(0,1)所以
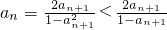 ,则
,则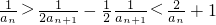
进而
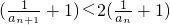 ,所以
,所以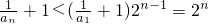
于是
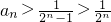
分析:由题意得
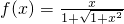 (x>0),令x=tanα
(x>0),令x=tanα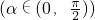 ,则
,则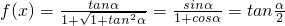 ,由于
,由于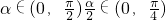 ,所以
,所以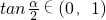 ,即函数f(x)的值域为(0,1)
,即函数f(x)的值域为(0,1)(1)由
 ,反解x可得
,反解x可得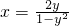 ,所以原函数的反函数
,所以原函数的反函数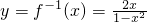 (0<x<1)
(0<x<1)(2)因为a1=a>0,an+1=f(an),n∈N*,所以
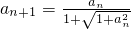
①利用放缩法.
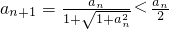 ,所以
,所以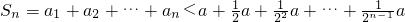 =
=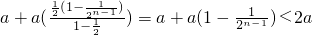
②因为an+1=f(an),所以an=f-1(an+1),所以
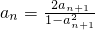 ,又由原函数的值域知an+1∈(0,1),所以
,又由原函数的值域知an+1∈(0,1),所以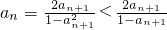 ,则
,则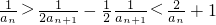 ,进而
,进而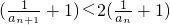 ,所以
,所以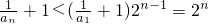 于是可得结论.
于是可得结论.点评:本题以新定义为载体,考查函数及反函数的求解,考查不等式的证明,解题的关键是适当放缩,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
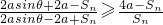 或
或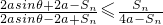 .
.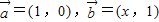 ,当x>0时,定义函数
,当x>0时,定义函数 .
.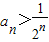 .
. ,当x>0时,定义函数
,当x>0时,定义函数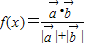 .
.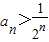 ;
; 或
或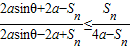 .
.