题目内容
设数列 的前
的前 项和为
项和为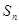 ,
, ,
, ,若
,若 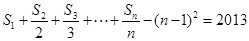 ,则
,则 的值为
的值为
| A.1007 | B.1006 | C.2012 | D.2013 |
A
解析试题分析:根据题意,由于数列 的前
的前 项和为
项和为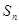 ,
, ,
,
然后根据累加法来得到数列的通项公式 ,那么可知
,那么可知 则可知参数n的值为1007 ,故选A.
则可知参数n的值为1007 ,故选A.
考点:数列的求和
点评:解决的关键是根据数列的通项公式以及前n项和的关系来求解数列的项,属于基础题。

练习册系列答案
相关题目
设 为等比数列
为等比数列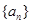 的前
的前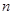 项和,若
项和,若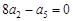 ,则
,则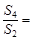 ( )
( )
A.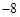 | B.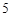 | C.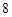 | D.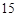 |
数列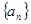 中,
中,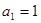 ,对所有的
,对所有的 都有
都有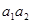 ……
…… ,则
,则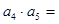 ( )
( )
A.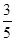 | B. | C. | D.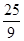 |
一个平面将空间分成两部分,两个平面将空间最多分成四部分,三个平面最多将空间分成八部分,…,由此猜测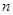 (
( )个平面最多将空间分成 ( )
)个平面最多将空间分成 ( )
A.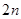 部分 部分 | B.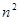 部分 部分 | C.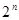 部分 部分 | D.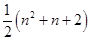 部分 部分 |
已知数列 中,
中, 前
前 项和为
项和为 ,且点
,且点 在一次函数
在一次函数 的图象上,则
的图象上,则 =( )
=( )
A. | B. | C. | D. |
已知正项数列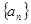 中,
中,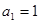 ,
,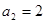 ,
,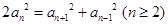 ,则
,则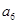 等于
等于
| A.16 | B.8 | C.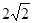 | D.4 |
数列 的通项公式为
的通项公式为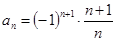 ,则
,则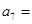 ( )
( )
| A.8 | B.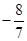 | C.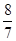 | D.7 |
 中,
中,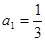 ,前
,前 项和
项和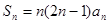 ,则数列
,则数列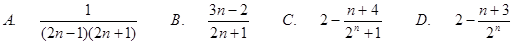
 )个音符的音符串,要求由音符?开始,相邻两个音符不能相同.例如
)个音符的音符串,要求由音符?开始,相邻两个音符不能相同.例如 时,排除的音符串是?∮,??;
时,排除的音符串是?∮,??; 时排出的音符串是?∮?,?∮?,???,??∮,….记这种含
时排出的音符串是?∮?,?∮?,???,??∮,….记这种含 个音符的所有音符串中,排在最后一个的音符仍是?的音符串的个数为
个音符的所有音符串中,排在最后一个的音符仍是?的音符串的个数为 .故
.故 .则(1)
.则(1) ;(2)
;(2) .
.