Question

如图，在长方体OABC—O₁A₁B₁C₁中,|OA|=2,|AB|=3,|AA₁|=2,E是BC中点.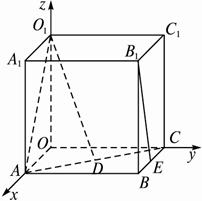

(1)求直线AO₁与B₁E所成角的大小;

(2)作O₁D⊥AC于D.求点O₁到点D的距离.

Answer 1

解：如图,建立空间直角坐标系.?

(1)由题设知,A(2,0,0),O₁(0,0,2).B₁(2,3,2),E(1,3,0).?

∴=(-2,0,2),=(-1,0,-2).?

∴cos〈,〉==-.?

∴AO₁与B₁E所成角的大小为arccos.?

(2)由题意得⊥,∥.?

∵C(0,3,0).设D(x,y,0),?

∴O₁D=(x,y,-2), =(x-2,y,0), =(-2,3,0).?

∴∴?

∴D(,,0).?

∴|O₁D|=||?

=

=.