Question

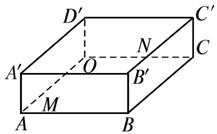
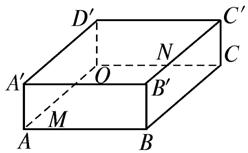
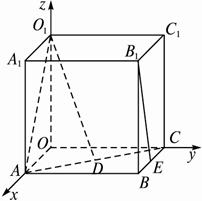
如图，在长方体OABC—O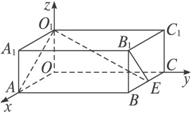₁A₁B₁C₁中，OA=2，AB=3，AA₁=2，E是BC的中点.

（1）求O₁E的长;

（2）求直线AO₁与B₁E所成的角.

Answer 1

解法一:(1)= +=.

∴||²=(++)²=||²+||²+||²=4+9+1=14.

∴||=14.

(2) =-+,=+=-.

·=(-+)·(-)= ||²-||²=-2.

||=.

||=.

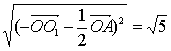∴cos〈,〉=.

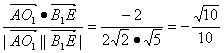∴〈,〉=arccos(-)=π-arccos.

故与所成的角为arccos.

解法二:以OA作为x轴正轴，OC作为y轴正轴，OO₁作为z轴正轴,建立空间直角坐标系.

 (1)O₁(0,0,2),E(1,3,0),

∴||=.

(2)A(2,0,0),B₁(2,3,2),则=(-2,0,2),=(-1,0,-2).

∴·=(-2)×(-1)+2×(-2)=-2,

||=,| |=.

∴cos〈, 〉=.

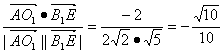故AO₁与B₁E₁所成的角为arccos.

解法三:(1)连结OE，

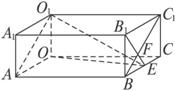
在Rt△OEC中,

OE=.

又由O₁O⊥平面OABC知O₁O⊥OE,

在Rt△O₁OE中，O₁E=.

(2)连结BC₁,交B₁E于F，

则BC₁∥AO₁.

设∠BFE=β,∠BEF=α,

则β即为直线AO₁与B₁E所成的角.

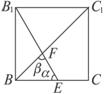
依题意，侧面B₁BCC₁为正方形,

在Rt△B₁BE中，tanα=2,B₁E=,sinα=,cosα=.

∴α=arcsin或arccos或arctan2.

∴β=π--α=-arcsin(或β=-arccos或β=-arctan2).