题目内容
设函数f(x)=kx2-kx-6+k.
(1)若对于k∈[-2,2],f(x)<0恒成立,求实数x的取值范围.
(2)若对于x∈[1,2],f(x)<0恒成立,求实数k的取值范围.
(1)若对于k∈[-2,2],f(x)<0恒成立,求实数x的取值范围.
(2)若对于x∈[1,2],f(x)<0恒成立,求实数k的取值范围.
(1)设f(x)=k(x2-x+1)-6=g(k),
则g(k)是关于k的一次函数,且一次项系数为x2-x+1…(2分)
法1、∵x2-x+1=(x-
)2+
>0∴g(k)在[-2,2]上递增.…(4分)
∴g(k)<0?g(2)=2(x2-x+1)-6<0∴解得x的取值范围为:-1<x<2…(6分)
法2、依题只须
?
∴-1<x<2
(2)法1、要使f(x)=k(x2-x+1)-6<0在x∈[1,2]上恒成立
则只须k<
在x∈[1,2]上恒成立;…(8分)
而当x∈[1,2]时:
=
≥
=2…(10分)
∴k<2…(12分)
法2、∵f(x)=k(x-
)2+
k-6<0在x∈[1,2]上恒成立
∴
或
或
综上解得:k<2
则g(k)是关于k的一次函数,且一次项系数为x2-x+1…(2分)
法1、∵x2-x+1=(x-
| 1 |
| 2 |
| 3 |
| 4 |
∴g(k)<0?g(2)=2(x2-x+1)-6<0∴解得x的取值范围为:-1<x<2…(6分)
法2、依题只须
|
|
(2)法1、要使f(x)=k(x2-x+1)-6<0在x∈[1,2]上恒成立
则只须k<
| 6 |
| x2-x+1 |
而当x∈[1,2]时:
| 6 |
| x2-x+1 |
| 6 | ||||
(x-
|
| 6 |
| 22-2+1 |
∴k<2…(12分)
法2、∵f(x)=k(x-
| 1 |
| 2 |
| 3 |
| 4 |
∴
|
|
|
综上解得:k<2

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
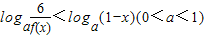 的解集.
的解集.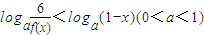 的解集.
的解集.