题目内容
设函数f(x)=kx+2,不等式[f(x)]2<36的解集为(-1,2).(1)求k的值;
(2)求不等式loga
| 6 | f(x) |
分析:(1)原不等式转化为:(kx+2)2<36,即k2x2+4kx-32<0,用韦达定理求解.
(2)根据f(x)=-4x+2将原不等式转化为:loga
<loga(1-x)再利用对数函数的单调性求解,要注意函数的定义域.
(2)根据f(x)=-4x+2将原不等式转化为:loga
| 6 |
| -4x+2 |
解答:解:(1)∵(kx+2)2<36,
即k2x2+4kx-32<0(
由题设可得:
,
解得k=-4
(2)f(x)=-4x+2
由loga
<loga(1-x)(0<a<1),
得loga
<loga(1-x)
则
,
即
∴原不等式的解集为{x|-
<x<
}
即k2x2+4kx-32<0(
由题设可得:
|
解得k=-4
(2)f(x)=-4x+2
由loga
| 6 |
| f(x) |
得loga
| 6 |
| -4x+2 |
则
|
即
|
∴原不等式的解集为{x|-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查一元二次不等式和对数不等式的解法,注意所涉及函数的定义域.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
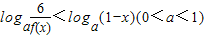 的解集.
的解集.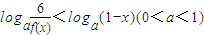 的解集.
的解集.