题目内容
已知点P(0,-3),点A在x轴上,点Q在y轴的正半轴上,点M满足
•
=0,
=-
,当点A在x轴上移动时,求动点M的轨迹方程.
| PA |
| AM |
| AM |
| 3 |
| 2 |
| MQ |
分析:设出点的坐标,利用点M满足
•
=0,
=-
,建立方程,化简整理可得结论.
| PA |
| AM |
| AM |
| 3 |
| 2 |
| MQ |
解答:解:设M(x,y)为所求轨迹上一点,设A(a,0),Q(0,b)(b>0),则
=(a,3),
=(x-a,y),
=(-x,b-y)
∵
•
=0,∴a(x-a)+3y=0①
∵
=-
,∴(x-a,y)=(
x,
(y-b))
∴
∴a=-
,b=
把a=-
代入①,整理可得y=
x2
∵b>0,∴x≠0
∴动点M的轨迹方程是y=
x2(x≠0).
| PA |
| AM |
| MQ |
∵
| PA |
| AM |
∵
| AM |
| 3 |
| 2 |
| MQ |
| 3 |
| 2 |
| 3 |
| 2 |
∴
|
∴a=-
| x |
| 2 |
| y |
| 3 |
把a=-
| x |
| 2 |
| 1 |
| 4 |
∵b>0,∴x≠0
∴动点M的轨迹方程是y=
| 1 |
| 4 |
点评:本题考查轨迹方程,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 •
• =0,
=0,
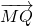 ,当点A在x轴上移动时,求动点M的轨迹方程.
,当点A在x轴上移动时,求动点M的轨迹方程.