题目内容
过抛物线y=x2上的点M(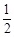 ,
, )的切线的倾斜角是( )
)的切线的倾斜角是( )
| A.30° | B.45° | C.60° | D.90° |
B
解析试题分析:.
∵点M(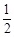 ,
, )满足抛物线y=x2,∴点M即为切点.
)满足抛物线y=x2,∴点M即为切点.
∵y=x2,∴y′=2x, x=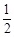 时,y′=1,
时,y′=1,
∵tan45°=1,∴过抛物线y=x2上的点M(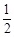 ,
, )的切线的倾斜角为45°,故选C.
)的切线的倾斜角为45°,故选C.
考点:利用导数研究曲线上某点切线方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数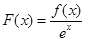 是定义在
是定义在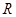 上的函数,其中
上的函数,其中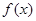 的导函数为
的导函数为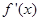 ,满足
,满足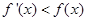 对于
对于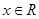 恒成立,则
恒成立,则
A.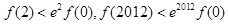 | B.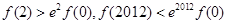 |
C.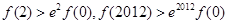 | D.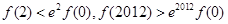 |
定义在R上的函数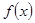 的图像如图所示,则关于
的图像如图所示,则关于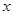 的不等式
的不等式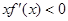 的解集为( )
的解集为( )
| A.(-2,-1)∪(1,2) | B.(-1,0)∪(1,+∞) |
| C.(-∞,-1)∪(0,1) | D.(-∞,-2)∪(2,+∞) |
曲线y=e-2x+1在点(0,2)处的切线与直线y=0和y=x围成的
三角形的面积为 ( ).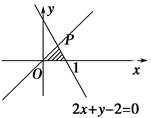
A.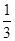 | B.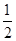 | C.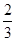 | D.1 |
函数f(x)=x2在区间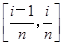 上( ).
上( ).
| A.f(x)的值变化很小 |
| B.f(x)的值变化很大 |
| C.f(x)的值不变化 |
| D.当n很大时,f(x)的值变化很小 |
已知曲线f(x)=ln x在点(x0,f(x0))处的切线经过点(0,-1),则x0的值为( )
A. | B.1 |
| C.e | D.10 |
函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式ex·f(x)>ex+1的解集为( )
| A.{x|x>0} | B.{x|x<0} |
| C.{x|x<-1或x>1} | D.{x|x<-1或0<x<1} |
 是
是 的导函数,
的导函数,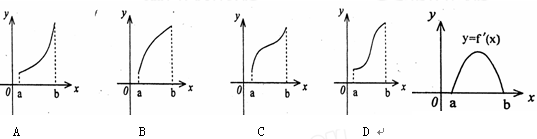
 的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列
的图像在点A(l,f(1))处的切线l与直线x十3y+2=0垂直,若数列 的前n项和为
的前n项和为 ,则S2013的值为( )
,则S2013的值为( )


