题目内容
(本小题满分l2分)
已知函数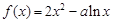
(1)若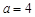 ,求函数
,求函数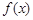 的极小值;
的极小值;
(2)设函数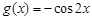 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量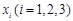 使得
使得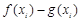 的值相等,若存在,请求出
的值相等,若存在,请求出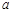 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?
(1)极小值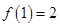 (2)不存在
(2)不存在
解析试题分析:(I)由已知得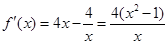 ,
,
则当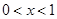 时
时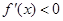 ,可得函数
,可得函数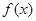 在
在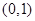 上是减函数,
上是减函数,
当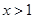 时
时 ,可得函数
,可得函数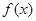 在
在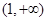 上是增函数,
上是增函数,
故函数的极小值为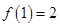 ;
;
(Ⅱ)若存在,设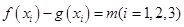 ,则对于某一实数
,则对于某一实数 ,方程
,方程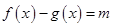 在
在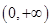 上有三个不同的实数根,设
上有三个不同的实数根,设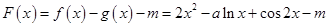 ,
,
则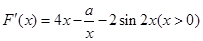 有两个不同的零点,即关于
有两个不同的零点,即关于 的方程
的方程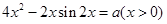 有两个不同的解
有两个不同的解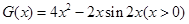 ,
,
则 ,
,
设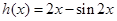 ,则
,则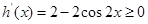 ,故
,故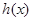 在
在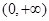 上单调递增,
上单调递增,
则当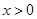 时
时 ,即
,即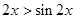 ,
,
又 ,则
,则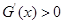 故
故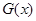 在
在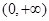 上是增函数,
上是增函数,
则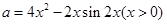 至多只有一个解,故不存。
至多只有一个解,故不存。
方法二:关于方程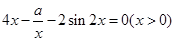 的解,
的解,
当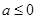 时,由方法一知
时,由方法一知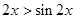 ,此时方程无解;
,此时方程无解;
当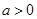 时,可以证明
时,可以证明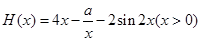 是增函数,此方程最多有一个解,故不存在。
是增函数,此方程最多有一个解,故不存在。
考点:利用导数研究函数的单调性;极值;函数的零点.
点评:本题考查函数的单调区间的求法,考查满足条件的实数的取值范围的求法.综合性强,难度大,具有一定的探索性.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
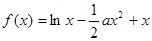
 时,求
时,求 的最大值;
的最大值;
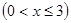 ,以其图象上任意一点
,以其图象上任意一点 为切点的切线的斜率
为切点的切线的斜率 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 时,方程
时,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值. 与
与 ,
, ,
, 所围成的平面图形的面积。
所围成的平面图形的面积。

 ;
; 的切线方程。
的切线方程。 ,点P(
,点P( ,0)是函数
,0)是函数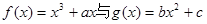 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.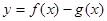 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求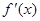 为f(x)的导函数,求证:
为f(x)的导函数,求证: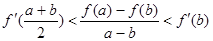
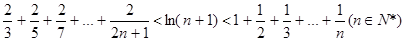
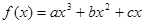 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间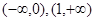 上是减函数,又
上是减函数,又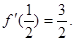
 的解析式;
的解析式;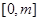 (m>0)上恒有
(m>0)上恒有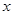 成立,求m的取值范围.
成立,求m的取值范围. .
. ,求
,求 的最小值;
的最小值; ,讨论函数
,讨论函数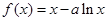 ,
,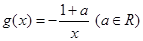 .
.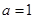 ,求函数
,求函数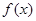 的极值;
的极值;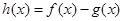 ,求函数
,求函数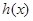 的单调区间;
的单调区间;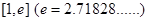 上不存在
上不存在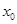 ,使得
,使得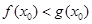 成立,求实数
成立,求实数 的取值范围.
的取值范围.