题目内容
(本小题满分12分)
设 ,点P(
,点P( ,0)是函数
,0)是函数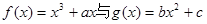 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(1)用 表示a,b,c;
表示a,b,c;
(2)若函数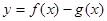 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求 的取值范围.
的取值范围.
(1) ,
, ,
, (2)
(2)
解析试题分析:(I)因为函数 ,
, 的图象都过点(
的图象都过点( ,0),所以
,0),所以 ,
,
即 .因为
.因为 所以
所以 .
.  ---2分
---2分
又因为 ,
, 在点(
在点( ,0)处有相同的切线,所以
,0)处有相同的切线,所以
而 --------4分
--------4分
将 代入上式得
代入上式得 因此
因此 故
故 ,
, ,
, ---6分
---6分
(II) .---7分
.---7分
当 时,函数
时,函数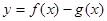 单调递减.
单调递减.
由 ,若
,若 ;若
;若  -------9分
-------9分
由题意,函数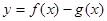 在(-1,3)上单调递减,则
在(-1,3)上单调递减,则 所以
所以 ---11分
---11分
所以 的取值范围为
的取值范围为 ----12分
----12分
考点:导数的几何意义;利用导数研究函数的单调性。
点评:利用导数求函数的单调区间,实质上就是求导数>0或导数<0的解集,这样问题就转化为了解不等式,尤其是解含参不等式更为常见。此题是导数中的典型题型,我们要熟练掌握。

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 。(Ⅰ)若函数
。(Ⅰ)若函数 在
在 处与直线
处与直线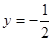 相切,①求实数
相切,①求实数 ,b的值;②求函数
,b的值;②求函数 上的最大值;(Ⅱ)当
上的最大值;(Ⅱ)当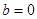 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数m的取值范围。
都成立,求实数m的取值范围。 其中
其中 ,曲线
,曲线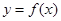 在点
在点 处的切线垂直于
处的切线垂直于 轴.
轴. 的值;
的值; 的极值.
的极值.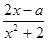 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.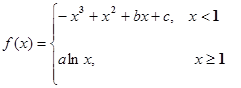 的图像过坐标原点
的图像过坐标原点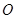 ,且在点
,且在点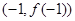 处的切线的斜率是
处的切线的斜率是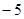 .
.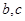 的值;
的值;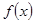 在区间
在区间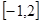 上的最大值;
上的最大值;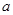 ,曲线
,曲线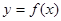 上是否存在两点
上是否存在两点 ,使得
,使得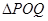 是以
是以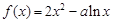
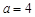 ,求函数
,求函数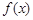 的极小值;
的极小值;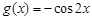 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量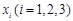 使得
使得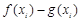 的值相等,若存在,请求出
的值相等,若存在,请求出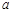 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由? 上,从原点向A(2,4)移动,如果直线OP,曲线
上,从原点向A(2,4)移动,如果直线OP,曲线 、
、 。
。
 时,求点P的坐标;
时,求点P的坐标;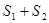 有最小值时,求点P的坐标和最小值.
有最小值时,求点P的坐标和最小值.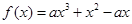 ,其中
,其中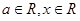 .
.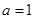 时,求函数
时,求函数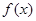 在
在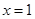 处的切线方程;
处的切线方程;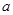 的取值范围;
的取值范围;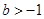 ,如果存在
,如果存在 ,使得函数
,使得函数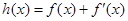
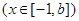 在
在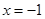 处取得最小值,试求
处取得最小值,试求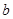 的最大值.
的最大值.