题目内容
函数y=Asin（wx+φ）+B在同一周期内的图象的最高点为（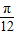
，3），最低点（
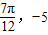），则其中w，φ的值分别为（ ）A．
，
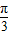
B．2，
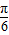
C．2，
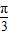
D．1，
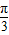
【答案】分析：依题意，可知B=-1，A=4，
T=
，从而可求w；再由
w+φ=2kπ+
即可求得φ．
解答：解：∵y=Asin（wx+φ）+B在同一周期内的图象的最高点为（
，3），最低点（
），
∴
T=
-
=
，
∴T=
=π，
∴w=2；
∴由
w+φ=2kπ+
得：φ=2kπ+
（k∈Z），令k=0得φ=
．
故选C．
点评：本题考查由y=Asin（ωx+φ）的图象求其解析式，求φ是难点，属于中档题．
T=，从而可求w；再由w+φ=2kπ+即可求得φ．解答：解：∵y=Asin（wx+φ）+B在同一周期内的图象的最高点为（
，3），最低点（），∴
T=-=，∴T=
=π，∴w=2；
∴由
w+φ=2kπ+得：φ=2kπ+（k∈Z），令k=0得φ=．故选C．
点评：本题考查由y=Asin（ωx+φ）的图象求其解析式，求φ是难点，属于中档题．
练习册系列答案
相关题目
，直线x=0是其图象的一条对称轴，求此函数的解析式．