题目内容
中心在原点,焦点坐标为F1(-1,0),F2(1,0),离心率为
的椭圆方程是( )
| 1 |
| 2 |
分析:由已知椭圆的中心在原点,焦点在x轴上,所以可设椭圆的标准方程为
+
=1,其中a2=b2+c2,c为半焦距,依题意可得a与c的值,计算b值即可
| x2 |
| a2 |
| y2 |
| b2 |
解答:解:∵椭圆中心在原点,焦点在x轴上,∴设椭圆的标准方程为
+
=1,
∵焦点坐标为F1(-1,0),F2(1,0),∴c=1,
∵离心率为
,∴
=
,∴a=2
∵a2=b2+c2,∴b2=3
∴椭圆的方程为
+
=1
故选C
| x2 |
| a2 |
| y2 |
| b2 |
∵焦点坐标为F1(-1,0),F2(1,0),∴c=1,
∵离心率为
| 1 |
| 2 |
| c |
| a |
| 1 |
| 2 |
∵a2=b2+c2,∴b2=3
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 3 |
故选C
点评:本题考察了椭圆的标准方程的求法,解题时要先定位,再定量,熟知参数的几何意义

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
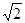 )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为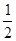 ,则椭圆方程为 ( )
,则椭圆方程为 ( )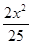 +
+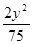 =1 B.
=1 B.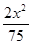 +
+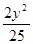 =1 C.
=1 C.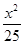 +
+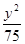 =1 D.
=1 D. +
+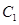 中心在原点,焦点坐标是
中心在原点,焦点坐标是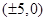 ,并且双曲线的离心率为
,并且双曲线的离心率为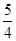 。
。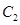 以双曲线
以双曲线 的椭圆被直线
的椭圆被直线 截得的弦的中点的横坐标为
截得的弦的中点的横坐标为 ,则椭圆方程为
,则椭圆方程为 B.
B.
 C.
C.  D.
D.
