题目内容
中心在原点,焦点坐标为(0, ±5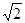 )的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为
)的椭圆被直线3x-y-2=0截得的弦的中点的横坐标为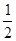 ,则椭圆方程为 ( )
,则椭圆方程为 ( )
A.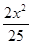 +
+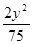 =1 B.
=1 B.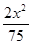 +
+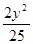 =1 C.
=1 C.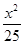 +
+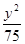 =1 D.
=1 D. +
+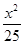 =1
=1
【答案】
C
【解析】主要考查椭圆的标准方程、几何性质,以及直线与椭圆的位置关系。
解:∵中心在原点,焦点坐标为(0, ±5 )∴长轴在y轴上
)∴长轴在y轴上
设椭圆方程 ,
,
设直线与椭圆的两个交点坐标为( ) , (
) , ( )
)
∵被直线y=3x-2截得弦的中点横坐标为
∴ =1;将弦端点坐标分别代入椭圆方程,并相减可得
=1;将弦端点坐标分别代入椭圆方程,并相减可得 =75,
=75, =25
=25
所以 +
+ =1即为所求,选C。
=1即为所求,选C。
思路拓展:利用待定系数法,首先假设椭圆的标准方程形式,与直线方程联立,利用弦中点坐标公式即根与系数的关系,建立方程组。这里利用的“点差法”求解。

练习册系列答案
相关题目
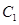 中心在原点,焦点坐标是
中心在原点,焦点坐标是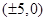 ,并且双曲线的离心率为
,并且双曲线的离心率为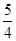 。
。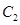 以双曲线
以双曲线 的椭圆被直线
的椭圆被直线 截得的弦的中点的横坐标为
截得的弦的中点的横坐标为 ,则椭圆方程为
,则椭圆方程为 B.
B.
 C.
C.  D.
D.
