题目内容
15.已知实数x,y满足:$\left\{\begin{array}{l}{x-y≤0}\\{x+y-4<0}\\{x-1≥0}\end{array}\right.$,则使等式(t+2)x+(t-1)y+2t+4=0成立的t取值范围为( )| A. | [-$\frac{5}{4}$,-$\frac{1}{2}$) | B. | (-∞,-$\frac{5}{4}$]∪(-$\frac{1}{2}$,+∞) | C. | [-$\frac{5}{4}$,1) | D. | [-$\frac{1}{2}$,1) |
分析 由题意作平面区域,从而化简可得t=$\frac{-2x+y-4}{x+y+2}$=1-$\frac{3}{\frac{y}{x+2}+1}$,而$\frac{y}{x+2}$几何意义是点A(-2,0)与阴影内的点的连线的斜率,从而结合图象解得.
解答 解:由题意作平面区域如下,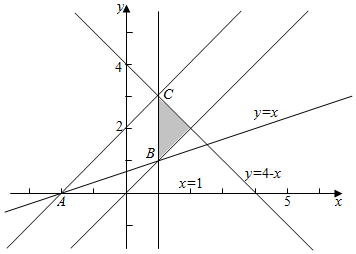 ,
,
∵(t+2)x+(t-1)y+2t+4=0,
∴t(x+y+2)+2x-y+4=0,
∴t=$\frac{-2x+y-4}{x+y+2}$=1-$\frac{3}{\frac{y}{x+2}+1}$,
$\frac{y}{x+2}$几何意义是点A(-2,0)与阴影内的点的连线的斜率,
而kAB=$\frac{1-0}{1+2}$=$\frac{1}{3}$,kAC=$\frac{3-0}{1+2}$=1,
故$\frac{1}{3}$≤$\frac{y}{x+2}$<1,
故$\frac{3}{2}$<$\frac{3}{\frac{y}{x+2}+1}$≤$\frac{9}{4}$,
故-$\frac{5}{4}$≤1-$\frac{3}{\frac{y}{x+2}+1}$<-$\frac{1}{2}$,
故选:A.
点评 本题考查了数形结合的思想应用,同时考查了转化的思想应用,关键在于化简得到t=1-$\frac{3}{\frac{y}{x+2}+1}$.

练习册系列答案
相关题目
6.已知a>1,b>1,且$\frac{1}{a-1}+\frac{1}{b-1}=1$,则a+4b的最小值为( )
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
7.若复数z+3=1-i,则复数z的共轭复数的模( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
4.命题“?x0∈R,使得x02+2x0+5=0”的否定是( )
| A. | ?x∈R,x2+2x+5=0 | B. | ?x∈R,x2+2x+5≠0 | C. | ?x∉R,x2+2x+5=0 | D. | ?x∉R,x2+2x+5≠0 |