题目内容
【题目】已知函数![]()
![]() .
.
(1)判断并证明函数的单调性;
(2)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(3)在(2)条件下,若对任意的正数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)增函数(2)![]() (3)
(3)![]() 的取值范围
的取值范围![]() ﹤
﹤![]()
【解析】
(1)在定义域上任取两个变量,且规定大小,再将对应的函数值作差变形看符号,利用单调性的定义即可得到结论.
(2)由f(x)是R上的奇函数所以f(x)+f(﹣x)=0求得.
(3)先求得a,结合(1)(2)得![]() ﹥
﹥![]() 对任意的
对任意的![]() ﹥0恒成立,利用二次函数图像及性质可得答案.
﹥0恒成立,利用二次函数图像及性质可得答案.
(1)函数![]() 为R上的增函数,证明如下:
为R上的增函数,证明如下:
函数![]() 的定义域为R,对任意
的定义域为R,对任意![]() ,
,
设![]() ﹤
﹤![]() ,
, ,
,
因为![]() 为R上的增函数,且
为R上的增函数,且![]() ﹤
﹤![]() ,所以
,所以![]() ﹤0,
﹤0,![]() ﹤0,
﹤0, ![]() ﹤
﹤![]() 函数
函数![]() 为R上的增函数。
为R上的增函数。
(2)∵函数![]() 为奇函数
为奇函数
∴![]() ,∴
,∴![]()
当![]() 时,
时,![]()
∴![]() ,
,
此时,函数![]() 为奇函数,满足题意。
为奇函数,满足题意。
所以![]() .
.
(3)因为函数![]() 为奇函数,从而不等式
为奇函数,从而不等式![]() ﹥0对任意的
﹥0对任意的![]() 恒成立等价于不等式
恒成立等价于不等式![]() ﹥
﹥![]() 对任意的
对任意的![]() 恒成立。
恒成立。
又因为在(—∞,+∞)上为增函数,
所以等价于不等式![]() ﹥
﹥![]() 对任意的
对任意的![]() ﹥0恒成立,
﹥0恒成立,
即2![]() ﹥0对任意的
﹥0对任意的![]() ﹥0恒成立.
﹥0恒成立.
所以必须有![]() ﹥0且△
﹥0且△![]() ﹤0;或
﹤0;或![]() ,
,
所以实数![]() 的取值范围
的取值范围![]() ﹤
﹤![]()

练习册系列答案
相关题目
【题目】现从某医院中随机抽取了7位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 98 | 88 | 96 | 91 | 90 | 92 | 96 |
| 9.9 | 8.6 | 9.5 | 9.0 | 9.1 | 9.2 | 9.8 |
(1)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);
(2)利用(1)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1)
附:回归直线方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
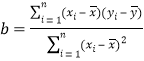 ,
,![]() .
.

