题目内容
设n∈N*,圆Cn:x2+y2=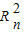 (Rn>0)与y轴正半轴的交点为M,与曲线
(Rn>0)与y轴正半轴的交点为M,与曲线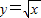 的交点为N(
的交点为N(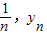 ),直线MN与x轴的交点为A(an,0).
),直线MN与x轴的交点为A(an,0).(1)用n表示Rn和an;
(2)求证:an>an+1>2;
(3)设Sn=a1+a2+a3+…+an,Tn=
 ,求证:
,求证: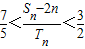 .
.
【答案】分析:(1)确定N、M的坐标,利用N在圆Cn:x2+y2= 上,直线MN与x轴的交点为A(an,0),即可用n表示Rn和an;
上,直线MN与x轴的交点为A(an,0),即可用n表示Rn和an;
(2)利用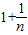 >
>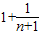 >2,
>2,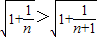 >1,即可证得结论;
>1,即可证得结论;
(3)先证当0≤x≤1时,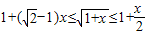 ,进而可得
,进而可得 ,从而
,从而 ,求和即可证得结论.
,求和即可证得结论.
解答:(1)解:∵N(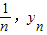 )在曲线
)在曲线 上,∴N(
上,∴N(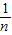 ,
, )
)
代入圆Cn:x2+y2= ,可得
,可得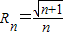 ,∴M(0,
,∴M(0, )
)
∵直线MN与x轴的交点为A(an,0).
∴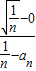 =
=
∴
(2)证明:∵ ,
,
∴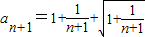 >2
>2
∵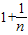 >
> ,
,
∴ >
>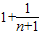 +
+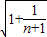
∴an>an+1>2;
(3)证明:先证当0≤x≤1时,
事实上,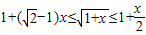 等价于
等价于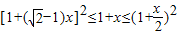
等价于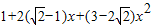 ≤1+x≤
≤1+x≤
等价于 ≤0≤
≤0≤
后一个不等式显然成立,前一个不等式等价于x2-x≤0,即0≤x≤1
∴当0≤x≤1时,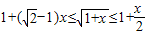
∴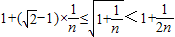
∴ (等号仅在n=1时成立)
(等号仅在n=1时成立)
求和得
∴ .
.
点评:本题考查数列与函数的综合,考查数列的通项,考查不等式的证明,证题的关键是证明当0≤x≤1时,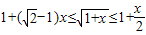 ,属于难题.
,属于难题.
 上,直线MN与x轴的交点为A(an,0),即可用n表示Rn和an;
上,直线MN与x轴的交点为A(an,0),即可用n表示Rn和an;(2)利用
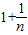 >
>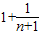 >2,
>2,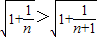 >1,即可证得结论;
>1,即可证得结论;(3)先证当0≤x≤1时,
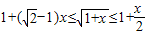 ,进而可得
,进而可得 ,从而
,从而 ,求和即可证得结论.
,求和即可证得结论.解答:(1)解:∵N(
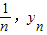 )在曲线
)在曲线 上,∴N(
上,∴N(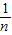 ,
, )
)代入圆Cn:x2+y2=
 ,可得
,可得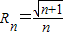 ,∴M(0,
,∴M(0, )
)∵直线MN与x轴的交点为A(an,0).
∴
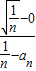 =
=
∴

(2)证明:∵
 ,
,
∴
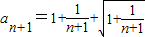 >2
>2∵
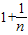 >
> ,
,
∴
 >
>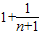 +
+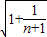
∴an>an+1>2;
(3)证明:先证当0≤x≤1时,

事实上,
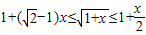 等价于
等价于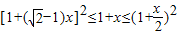
等价于
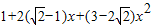 ≤1+x≤
≤1+x≤
等价于
 ≤0≤
≤0≤
后一个不等式显然成立,前一个不等式等价于x2-x≤0,即0≤x≤1
∴当0≤x≤1时,
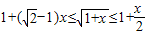
∴
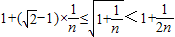
∴
 (等号仅在n=1时成立)
(等号仅在n=1时成立)求和得

∴
 .
.点评:本题考查数列与函数的综合,考查数列的通项,考查不等式的证明,证题的关键是证明当0≤x≤1时,
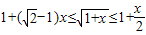 ,属于难题.
,属于难题. 
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
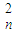 (Rn>0)与y轴正半轴的交点为M,与曲线y=
(Rn>0)与y轴正半轴的交点为M,与曲线y=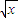 的交点为N(xn,yn),直线MN与x轴的交点为A(an,0).
的交点为N(xn,yn),直线MN与x轴的交点为A(an,0).