题目内容
已知 是以点
是以点 为圆心的圆
为圆心的圆 上的动点,定点
上的动点,定点 .点
.点 在
在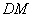 上,点
上,点 在
在 上,且满足
上,且满足 .动点
.动点 的轨迹为曲线
的轨迹为曲线 。
。
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)线段 是曲线
是曲线 的长为
的长为 的动弦,
的动弦, 为坐标原点,求
为坐标原点,求 面积
面积 的取值范围。
的取值范围。
【答案】
解:(Ⅰ)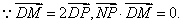
∴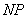 为
为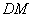 的垂直平分线,∴
的垂直平分线,∴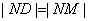 ,
,
又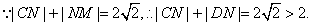 (2分)
(2分)
∴动点 的轨迹是以点
的轨迹是以点 为焦点的长轴为
为焦点的长轴为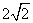 的椭圆.
的椭圆.
∴轨迹E的方程为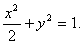 (4分)
(4分)
(Ⅱ) 解法一∵线段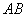 的长等于椭圆短轴的长,要使三点
的长等于椭圆短轴的长,要使三点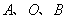 能构成三角形,
能构成三角形,
则弦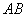 不能与
不能与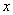 轴垂直,故可设直线
轴垂直,故可设直线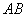 的方程为
的方程为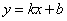 ,
,
由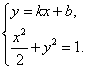 ,消去
,消去 ,并整理,得
,并整理,得

设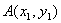 ,
, ,则
,则
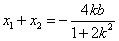 ,
,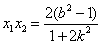 。
(6分)
。
(6分)
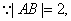
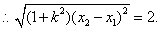
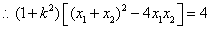 ,
,
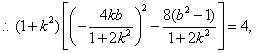
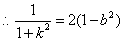 ,
,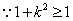 ,
,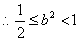 .
(8分)
.
(8分)
又点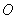 到直线
到直线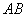 的距离
的距离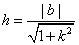 ,
,
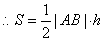
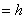 ,
,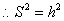
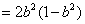
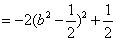 (10分)
(10分)
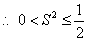 ,
,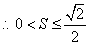 .
(12分)
.
(12分)
解法二:∵线段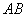 的长等于椭圆短轴的长,要使三点
的长等于椭圆短轴的长,要使三点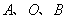 能构成三角形,则弦
能构成三角形,则弦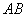 不能与
不能与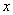 轴垂直,故可设直线
轴垂直,故可设直线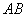 的方程为
的方程为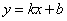 ,
,
由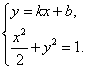 ,消去
,消去 ,并整理,得
,并整理,得

设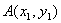 ,
, ,则
,则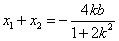 ,
,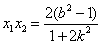 (8分)
(8分)
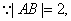
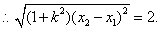
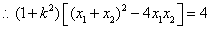 ,
,
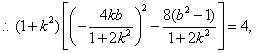
 (10分)
(10分)
又点 到直线
到直线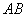 的距离
的距离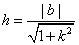 ,
,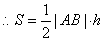
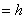 。
。
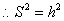
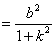
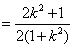
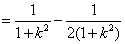
设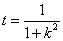 ,则
,则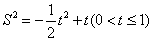 ,
,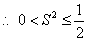 ,
,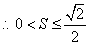 . (12分)
. (12分)
(注:上述两种解法用均值不等式求解可参照此标准给分)
评析:解析几何中的轨迹问题一直是出题的重要方向,圆锥曲线不考察第二定义以后,由圆在内构造的轨迹问题成为主要的出题方向(容易构造),需要考生注意平时积累;直线与圆、圆锥曲线间的位置关系的判定、证明、求值能有效考察考生的运算能力;

练习册系列答案
相关题目