题目内容
(14分)已知![]() 是以点
是以点![]() 为圆心的圆
为圆心的圆![]() 上的动点,定点
上的动点,定点![]() .点
.点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且满足
上,且满足![]() .动点
.动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)线段![]() 是曲线
是曲线![]() 的长为
的长为![]() 的动弦,
的动弦,![]() 为坐标原点,求
为坐标原点,求![]() 面积
面积![]() 的取值范围.
的取值范围.
解析:(Ⅰ)![]()
∴![]() 为
为![]() 的垂直平分线,∴
的垂直平分线,∴![]() ,
,
又![]() ………………………………3分
………………………………3分
∴动点![]() 的轨迹是以点
的轨迹是以点![]() 为焦点的长轴为
为焦点的长轴为![]() 的椭圆.
的椭圆.
∴轨迹E的方程为![]() ………………………………………………………5分
………………………………………………………5分
(Ⅱ) 解法一∵线段![]() 的长等于椭圆短轴的长,要使三点
的长等于椭圆短轴的长,要使三点![]() 能构成三角形,则弦
能构成三角形,则弦![]() 不能与
不能与![]() 轴垂直,故可设直线
轴垂直,故可设直线![]() 的方程为
的方程为![]() ,
,
由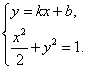 ,消去
,消去![]() ,并整理,得
,并整理,得
![]()
设![]() ,
,![]() ,则
,则
![]() ,
,![]() …………………………………………8分
…………………………………………8分
![]()
![]()
![]() ,
,
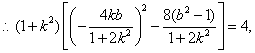
![]() , ………………………………………………………11分
, ………………………………………………………11分
![]()
![]() . ……………………………………12分
. ……………………………………12分
又点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
![]()
![]()
![]()
![]()
![]() ……………………………………………13分
……………………………………………13分
![]() ,
,
![]() . …………………………………………14分
. …………………………………………14分
解法二:∵线段![]() 的长等于椭圆短轴的长,要使三点
的长等于椭圆短轴的长,要使三点![]() 能构成三角形,则弦
能构成三角形,则弦![]() 不能与
不能与![]() 轴垂直,故可设直线
轴垂直,故可设直线![]() 的方程为
的方程为![]() ,
,
由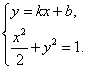 ,消去
,消去![]() ,并整理,得
,并整理,得
![]()
设![]() ,
,![]() ,则
,则
![]() ,
,![]() …………………………………………8分
…………………………………………8分
![]()
![]()
![]() ,
,
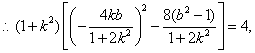
![]() ………………………………………………………11分
………………………………………………………11分
又点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
设![]() ,则
,则
![]()
![]() ,
,
![]() . ……………………………………………………14分
. ……………………………………………………14分
(注:上述两种解法用均值不等式求解可参照此标准给分)

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
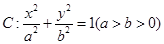 过点
过点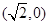 ,且离心率为
,且离心率为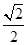 .
.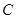 的方程;
的方程;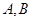 为椭圆
为椭圆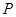 是椭圆
是椭圆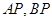 分别交直线
分别交直线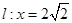 于
于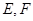 两点.
两点. 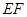 为直径的圆恒过
为直径的圆恒过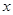 轴上的定点.
轴上的定点. 的焦点
的焦点 为其一个焦点,以双曲线
为其一个焦点,以双曲线 的焦点
的焦点 为顶点。
为顶点。 ,且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求
,且C、D分别为椭圆的上顶点和右顶点,点M是线段CD上的动点,求 的取值范围。
的取值范围。 的焦点
的焦点 为其一个焦点,以双曲线
为其一个焦点,以双曲线 的焦点
的焦点 为顶点。
为顶点。 ,且
,且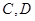 分别为椭圆的上顶点和右顶点,点
分别为椭圆的上顶点和右顶点,点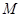 是线段
是线段 上的动点,求
上的动点,求 的取值范围。
的取值范围。