题目内容
已知函数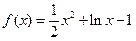 .
.
(1)求函数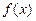 在区间
在区间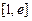 (
(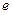 为自然对数的底)上的最大值和最小值;
为自然对数的底)上的最大值和最小值;
(2)求证:在区间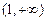 上,函数
上,函数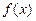 的图象在函数
的图象在函数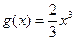 的图象的下方;
的图象的下方;
(3)求证: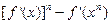 ≥
≥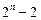
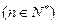 .
.
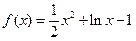 .
.(1)求函数
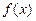 在区间
在区间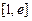 (
(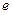 为自然对数的底)上的最大值和最小值;
为自然对数的底)上的最大值和最小值;(2)求证:在区间
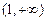 上,函数
上,函数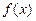 的图象在函数
的图象在函数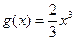 的图象的下方;
的图象的下方;(3)求证:
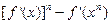 ≥
≥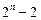
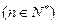 .
.(1)
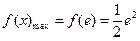 ,
,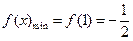 (2)证明见解析
(2)证明见解析(3)证明见解析
(1)∵

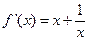 -------------------------------------1分
-------------------------------------1分当
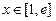 时,
时,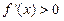
∴函数
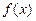 在
在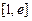 上为增函数-----------------------------------------3分
上为增函数-----------------------------------------3分∴
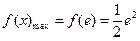 ,
,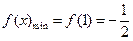 --------------------------4分
--------------------------4分(2)证明:令
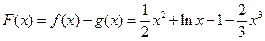
则
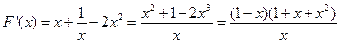
∵当
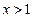 时
时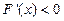 ,∴函数
,∴函数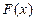 在区间
在区间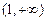 上为减函数
上为减函数∴
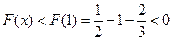
即在
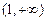 上,
上,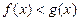
∴在区间
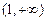 上,函数
上,函数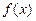 的图象在函数
的图象在函数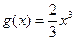 的图象的下方-----8分
的图象的下方-----8分(3)证明:∵
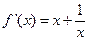
当
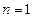 时,不等式显然成立
时,不等式显然成立当
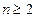 时
时∵
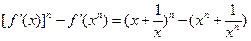 =
=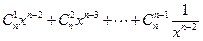 -----①
-----①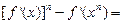
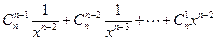 -------------②-----10分
-------------②-----10分①+②得
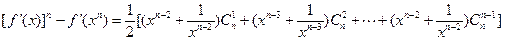
≥
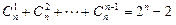 (当且仅当
(当且仅当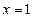 时“=”成立)---------------13分
时“=”成立)---------------13分∴当
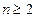 时,不等式成立
时,不等式成立综上所述得
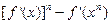 ≥
≥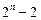
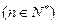 .--------------------------14分
.--------------------------14分
练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
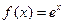 (
(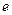 为自然对数的底数),
为自然对数的底数),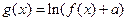 (
(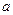 为常数),
为常数),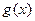 是实数集
是实数集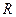 上的奇函数.(Ⅰ)求证:
上的奇函数.(Ⅰ)求证: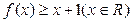 ;
;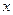 的方程:
的方程: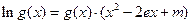
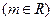 的根的个数;
的根的个数;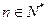 ,证明:
,证明: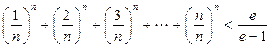 (
(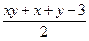 .
.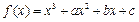 在
在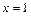 与
与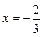 时都取得极值.
时都取得极值.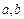 的值;(2)若
的值;(2)若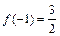 ,求
,求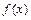 的单调区间和极值;
的单调区间和极值; x3 +
x3 +  ax2 + 2ax (x∈R). (Ⅰ)当a = 1时,求函数f (x)的单调递增区间; (Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由; (Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.
ax2 + 2ax (x∈R). (Ⅰ)当a = 1时,求函数f (x)的单调递增区间; (Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由; (Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.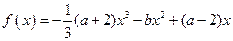 。
。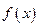 在
在 处取得极值,且
处取得极值,且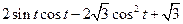 试求实数
试求实数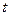 的取值范围;
的取值范围;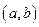 ,试求出点P的轨迹所形成的图形的面积S。
,试求出点P的轨迹所形成的图形的面积S。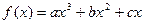 (
(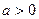 )的图象关于原点对称,
)的图象关于原点对称,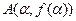 、
、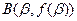 分别为函数
分别为函数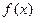 的极大值点和极小值点,且|AB|=2,
的极大值点和极小值点,且|AB|=2, .
.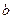 的值;
的值; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.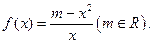
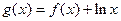 ,当m≥
,当m≥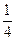 时,求g(x)在[
时,求g(x)在[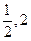 ]上的最大值;
]上的最大值;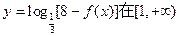 上是单调减函数,求实数m的取值范围.
上是单调减函数,求实数m的取值范围.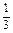 是f(x)的极值点,求f(x)在[1,a]上的最大值;
是f(x)的极值点,求f(x)在[1,a]上的最大值;