题目内容
设变量x,y满足约束条件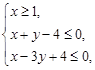 则目标函数z=3x-y的最大值为
则目标函数z=3x-y的最大值为
A.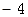 | B.0 | C. | D.4 |
D
解析试题分析:画出可行域(如图),直线3x-y=0,平移直线3x-y=0,分析可知当直线经过y=4-x与x-3y+4=0的交点A(2,2)时,z最大值为4,故选D。
考点:本题主要考查简单线性规划的应用。
点评:简单题,简单线性规划问题,已是高考必考题型,注意遵循“画,移,解,答”等步骤。

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
直线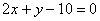 与不等式组
与不等式组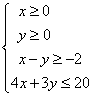 表示的平面区域的公共点有
表示的平面区域的公共点有
A.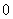 个 个 | B.1个 | C.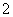 个 个 | D.无数个 |
在平面直角坐标系中,若不等式组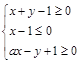 (
(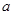 为常数)所表示的平面区域的面积等于
为常数)所表示的平面区域的面积等于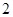 ,则
,则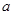 的值为
的值为
| A.-5 | B.1 | C.2 | D.3 |
若不等式组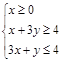 所表示的平面区域被直线
所表示的平面区域被直线 分为面积相等的两部分,则
分为面积相等的两部分,则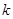 的值是( )
的值是( )
A.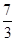 | B.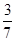 | C.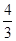 | D.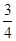 |
如图,目标函数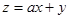 的可行域为四边形
的可行域为四边形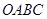 (含边界),若
(含边界),若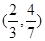 是该目标函数
是该目标函数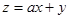 的最优解,则实数
的最优解,则实数 的取值范围是
的取值范围是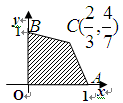
A. | B. | C.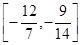 | D.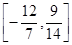 |
若 则目标函数
则目标函数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设 满足约束条件
满足约束条件 ,则
,则 的最大值为( )
的最大值为( )
| A.5 | B.7 | C.3 | D.-8 |
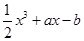 在区间[-1,1]上有且仅有一个零点的概率为
在区间[-1,1]上有且仅有一个零点的概率为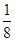

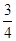
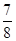
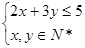 B.
B.
 D.
D.