题目内容
如图,目标函数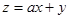 的可行域为四边形
的可行域为四边形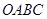 (含边界),若
(含边界),若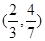 是该目标函数
是该目标函数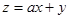 的最优解,则实数
的最优解,则实数 的取值范围是
的取值范围是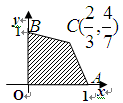
A. | B. | C.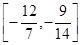 | D.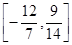 |
C
解析试题分析:根据已知的可行域,及再用角点法,若目标函数z=ax-y在点C处取得最优解,根据在C点有最优解,则过C的直线z=ax-y与可行域只有一个交点或与边界AC、BC所在的直线重合,利用直线的斜率之间的关系,即求出实数a的取值范围。直线z=ax-y的斜率为a,若C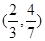
是该目标函数z=ax-y的最优解,则过C的直线z=ax-y与可行域只有一个交点或与边界AC、BC所在的直线重合,
因为 ,故选C.
,故选C.
考点:线性规划的最优解
点评:本题主要考查了简单的线性规划,以及利用几何意义求最值的方法反求参数的范围,属于基础题

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨,那么该企业可获得最大利润是 ( )
| A.12万元 | B.20万元 | C.25万元 | D.27万元 |
已知实数 满足不等式组
满足不等式组 ,则
,则 的最大值是
的最大值是
| A.0 | B.3 | C.4 | D.5 |
已知变量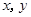 满足约束条件
满足约束条件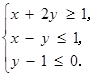 则
则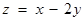 的最大值为
的最大值为
A.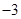 | B. | C. | D.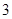 |
设变量x,y满足约束条件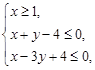 则目标函数z=3x-y的最大值为
则目标函数z=3x-y的最大值为
A.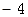 | B.0 | C. | D.4 |
设 为坐标原点,
为坐标原点, ,若
,若 满足
满足 ,则
,则 的最大值为
的最大值为
| A.4 | B.6 | C.8 | D.10 |
设变量 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
设变量x,y满足约束条件: .则目标函数z=2x+3y的最小值为( )
.则目标函数z=2x+3y的最小值为( )
| A.6 | B.7 | C.8 | D.23 |
 ,
, 满足约束条件
满足约束条件 ,若目标函数
,若目标函数 (
( ,
, )的最大值为12,则
)的最大值为12,则 的取值范围是( )
的取值范围是( )


