题目内容
9.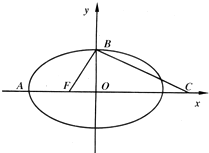 如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为$\frac{1}{2}$.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:$x+\sqrt{3}y+3=0$相切.则椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为$\frac{1}{2}$.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:$x+\sqrt{3}y+3=0$相切.则椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
分析 由已知设F(-c,0),B(0,$\sqrt{3}c$),由圆与直线相切的性质和点到直线的距离公式能求出c=1,由此能求出椭圆方程.
解答 解:由已知设F(-c,0),B(0,$\sqrt{3}c$),
∵kBF=$\sqrt{3}$,kBC=-$\frac{{\sqrt{3}}}{3}$,C(3c,0),
且圆M的方程为(x-c)2+y2=4c2,圆M与直线l1:x+$\sqrt{3}$u+3=0相切,
∴$\frac{{|{1×c+\sqrt{3}×0+3}|}}{{\sqrt{1+3}}}=2c$,解得c=1,
∴所求的椭圆方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
故答案为:$\frac{x^2}{4}+\frac{y^2}{3}=1$.
点评 本题考查椭圆方程的求法,是中档题,解题时要认真审题,注意圆与直线相切的性质和点到直线的距离公式的合理运用.

练习册系列答案
相关题目
20.在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高二年级有男生1000人,女生800人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高二年级抽取了45名学生的测评结果,并作出频数统计表如下:
表一:男生
表二:女生
(1)计算x,y的值;
(2)由表一表二中统计数据完成下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
表一:男生
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
(2)由表一表二中统计数据完成下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
| 男生 | 女生 | 总计 | |
| 优秀 | 15 | 15 | 30 |
| 非优秀 | |||
| 总计 | 45 |
4.设数列{an}的前n项和为Sn,若Sn=n2+2n(n∈N*),则$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$=( )
| A. | $\frac{1}{3}-\frac{1}{2n+1}$ | B. | $\frac{1}{3}-\frac{1}{2n+3}$ | C. | $\frac{1}{6}-\frac{1}{4n+3}$ | D. | $\frac{1}{6}-\frac{1}{4n+6}$ |
 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm),若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118)内该厂可获利分别为10,30,20,10(单位:元),现在该厂生产的产品中随机抽取200件测量它们的直径,得到如图所示的频率直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm),若生产一件产品A的直径位于区间[110,112),[112,114),[114,116),[116,118)内该厂可获利分别为10,30,20,10(单位:元),现在该厂生产的产品中随机抽取200件测量它们的直径,得到如图所示的频率直方图.