题目内容
已知数列an满足递推关系式:2an+1=1-an2(n≥1,n∈N),且0<a1<1.(1)求a3的取值范围;
(2)用数学归纳法证明:
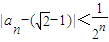 (n≥3,n∈N);
(n≥3,n∈N);(3)若
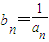 ,求证:
,求证: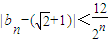 (n≥3,n∈N).
(n≥3,n∈N).
【答案】分析:(1)由题设知 ,且a1∈(0,1),由二次函数性质可知a2∈(0,
,且a1∈(0,1),由二次函数性质可知a2∈(0, ).由此能求出a3的取值范围;(2)用数学归纳法进行证明,证明过程中要注意合理地进行等价转化.
).由此能求出a3的取值范围;(2)用数学归纳法进行证明,证明过程中要注意合理地进行等价转化.
(3)由 变形为:
变形为: ,由此入手能够得到证明.
,由此入手能够得到证明.
解答:解:(1)∵ ,且a1∈(0,1),由二次函数性质可知a2∈(0,
,且a1∈(0,1),由二次函数性质可知a2∈(0, ).
).
∵ 及
及 ∴
∴
(2)证明:①在(1)的过程中可知n=3时, ,
,
则- ,
,
于是当n=3时, 成立.
成立.
②假设在n=k(k≥3)时, (*)成立,即
(*)成立,即 .
.
则当n=k+1时, =
= ,
,
其中0<
于是 ,
,
从而n=k+1时(*)式得证.
综合①②可知:n≥3,n∈{N}时 .
.
(3)由 变形为:
变形为: ,
,
而由 (n≥3,n∈N)
(n≥3,n∈N)
可知: 在n≥3上恒成立,
在n≥3上恒成立,
于是 ,
,
又∵ ,∴
,∴ ,
,
从而原不等式 (n≥3,n∈N)得证.(14分)
(n≥3,n∈N)得证.(14分)
点评:本题考查数列的性质和应用,解题时要认真审题,挖掘题设中的隐含条件,注意数学归纳法的解题过程.
 ,且a1∈(0,1),由二次函数性质可知a2∈(0,
,且a1∈(0,1),由二次函数性质可知a2∈(0, ).由此能求出a3的取值范围;(2)用数学归纳法进行证明,证明过程中要注意合理地进行等价转化.
).由此能求出a3的取值范围;(2)用数学归纳法进行证明,证明过程中要注意合理地进行等价转化.(3)由
 变形为:
变形为: ,由此入手能够得到证明.
,由此入手能够得到证明.解答:解:(1)∵
 ,且a1∈(0,1),由二次函数性质可知a2∈(0,
,且a1∈(0,1),由二次函数性质可知a2∈(0, ).
).∵
 及
及 ∴
∴
(2)证明:①在(1)的过程中可知n=3时,
 ,
,则-
 ,
,于是当n=3时,
 成立.
成立.②假设在n=k(k≥3)时,
 (*)成立,即
(*)成立,即 .
.则当n=k+1时,
 =
= ,
,其中0<

于是
 ,
,从而n=k+1时(*)式得证.
综合①②可知:n≥3,n∈{N}时
 .
.(3)由
 变形为:
变形为: ,
,而由
 (n≥3,n∈N)
(n≥3,n∈N)可知:
 在n≥3上恒成立,
在n≥3上恒成立,于是
 ,
,又∵
 ,∴
,∴ ,
,从而原不等式
 (n≥3,n∈N)得证.(14分)
(n≥3,n∈N)得证.(14分)点评:本题考查数列的性质和应用,解题时要认真审题,挖掘题设中的隐含条件,注意数学归纳法的解题过程.

练习册系列答案
相关题目
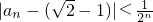 (n≥3,n∈N);
(n≥3,n∈N);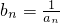 ,求证:
,求证: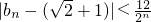 (n≥3,n∈N).
(n≥3,n∈N).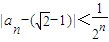 (n≥3,n∈N);
(n≥3,n∈N);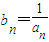 ,求证:
,求证: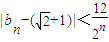 (n≥3,n∈N).
(n≥3,n∈N).