题目内容
已知数列an满足递推关系式:2an+1=1-an2(n≥1,n∈N),且0<a1<1.
(1)求a3的取值范围;
(2)用数学归纳法证明:|an-(
-1)|<
(n≥3,n∈N);
(3)若bn=
,求证:|bn-(
+1)|<
(n≥3,n∈N).
(1)求a3的取值范围;
(2)用数学归纳法证明:|an-(
| 2 |
| 1 |
| 2n |
(3)若bn=
| 1 |
| an |
| 2 |
| 12 |
| 2n |
(1)∵a2=
(1-a21),且a1∈(0,1),由二次函数性质可知a2∈(0,
).
∵a3=
(1-
)及a2∈(0,
)∴a3∈(
,
).(3分)
(2)证明:①在(1)的过程中可知n=3时,
<a3<
,
则-
<
-(
-1)<a3-(
-1)<
-(
-1)<
,
于是当n=3时,|an-(
-1)|<
成立.
②假设在n=k(k≥3)时,|an-(
-1)|<
(*)成立,即|ak-(
-1)|<
.
则当n=k+1时,|ak+1-(
-2)|=|
-
-(
-1)|=
|ak-(
-1)|•|ak+
-1|,
其中0<ak+
-1<2(
-1)+
<1(k≥3)
于是|ak+1-(
-1)|<
|ak-(
-1)|<
,
从而n=k+1时(*)式得证.
综合①②可知:n≥3,n∈{N}时|an-(
-1)|<
.
(3)由|an-(
-1)|<
(n≥3)变形为:|
-
|<
•
=
•
,
而由
-1-
<an<
-1+
(n≥3,n∈N)
可知:
-1-
<an<
+1+
在n≥3上恒成立,
于是
<
,
<
<12,
又∵|an-(
-1)|<
,∴|
-(
+1)|<
,
从而原不等式|bn-(
+1)|<
(n≥3,n∈N)得证.(14分)
| 1 |
| 2 |
| 1 |
| 2 |
∵a3=
| 1 |
| 2 |
| a | 22 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| 2 |
(2)证明:①在(1)的过程中可知n=3时,
| 3 |
| 8 |
| 1 |
| 2 |
则-
| 1 |
| 8 |
| 3 |
| 8 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 8 |
于是当n=3时,|an-(
| 2 |
| 1 |
| 2n |
②假设在n=k(k≥3)时,|an-(
| 2 |
| 1 |
| 2n |
| 2 |
| 1 |
| 2k |
则当n=k+1时,|ak+1-(
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a | 2k |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
其中0<ak+
| 2 |
| 2 |
| 1 |
| 2k |
于是|ak+1-(
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2k+1 |
从而n=k+1时(*)式得证.
综合①②可知:n≥3,n∈{N}时|an-(
| 2 |
| 1 |
| 2n |
(3)由|an-(
| 2 |
| 1 |
| 2n |
| 1 | ||
|
| 1 |
| an |
| 1 |
| 2n |
| 1 | ||
(
|
| ||
| 2n |
| 1 |
| |an| |
而由
| 2 |
| 1 |
| 2n |
| 2 |
| 1 |
| 2n |
可知:
| 2 |
| 1 |
| 8 |
| 2 |
| 1 |
| 8 |
于是
| 1 |
| an |
| 1 | ||||
|
| ||
| an |
| ||||
|
又∵|an-(
| 2 |
| 1 |
| 2n |
| 1 |
| an |
| 2 |
| 12 |
| 2n |
从而原不等式|bn-(
| 2 |
| 12 |
| 2n |

练习册系列答案
相关题目
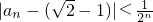 (n≥3,n∈N);
(n≥3,n∈N);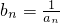 ,求证:
,求证: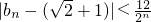 (n≥3,n∈N).
(n≥3,n∈N).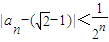 (n≥3,n∈N);
(n≥3,n∈N);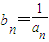 ,求证:
,求证: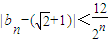 (n≥3,n∈N).
(n≥3,n∈N).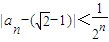 (n≥3,n∈N);
(n≥3,n∈N);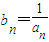 ,求证:
,求证: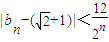 (n≥3,n∈N).
(n≥3,n∈N).