题目内容
14.已知$|\overrightarrow a|=3,|\overrightarrow b|=4$,且$\overrightarrow a$与$\overrightarrow b$的夹角θ=120°,求(1)$\overrightarrow{a}•\overrightarrow{b}$;
(2)$|\overrightarrow a+\overrightarrow b|$;
(3)($\overrightarrow a$-$\overrightarrow b$)在$\overrightarrow{a}方向上$的射影.
分析 (1)代入数量积公式计算;
(2)求出($\overrightarrow{a}+\overrightarrow{b}$)2,开方即得出答案;
(3)求出$\overrightarrow{a}-\overrightarrow{b}$与$\overrightarrow{a}$的夹角,代入公式计算.
解答 解:(1)$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos120°=3×4×(-$\frac{1}{2}$)=-6.
(2)∵($\overrightarrow{a}+\overrightarrow{b}$)2=$\overrightarrow{a}$2+2$\overrightarrow{a}•\overrightarrow{b}$+$\overrightarrow{b}$2=9-12+16=13,
∴$|\overrightarrow a+\overrightarrow b|$=$\sqrt{13}$.
(3))∵($\overrightarrow{a}-\overrightarrow{b}$)2=$\overrightarrow{a}$2-2$\overrightarrow{a}•\overrightarrow{b}$+$\overrightarrow{b}$2=9+12+16=37,
∴|$\overrightarrow{a}-\overrightarrow{b}$|=$\sqrt{37}$.
($\overrightarrow{a}-\overrightarrow{b}$)•$\overrightarrow{a}$=$\overrightarrow{a}$2-$\overrightarrow{a}•\overrightarrow{b}$=9+6=15,
∴cos<$\overrightarrow{a}-\overrightarrow{b}$,$\overrightarrow{a}$>=$\frac{(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}-\overrightarrow{b}|•|\overrightarrow{a}|}$=$\frac{15}{3\sqrt{37}}$=$\frac{5\sqrt{37}}{37}$,
∴($\overrightarrow a$-$\overrightarrow b$)在$\overrightarrow{a}方向上$的射影为|$\overrightarrow{a}-\overrightarrow{b}$|•cos<$\overrightarrow{a}-\overrightarrow{b}$,$\overrightarrow{a}$>=$\sqrt{37}$×$\frac{5\sqrt{37}}{37}$=5.
点评 本题考查了平面向量的数量积和模运算,属于基础题.

| A. | $\frac{π}{6}$ | B. | $\frac{π}{5}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{9}$ |
| A. | |3m-4n-5|=10 | B. | |3m-4n+5|=10 | C. | 3m-4n-5=10 | D. | 3m-4n+5=10 |
| A. | $(-3,-\frac{π}{2})∪(0,1)∪(\frac{π}{2},3)$ | B. | $(-\frac{π}{2},-1)∪(0,1)∪(\frac{π}{2},3)$ | C. | (-3,-1)∪(0,1)∪(1,3) | D. | $(-3,-\frac{π}{2})∪(0,1)∪(1,3)$ |
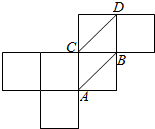 如图是一个正方体的展开图,在原正方体中直线AB与CD的位置关系是异面.
如图是一个正方体的展开图,在原正方体中直线AB与CD的位置关系是异面.