Question

将边长为a的正方形ABCD沿对角线AC折成直二面角，则BD的长度为（　　）

• A．

  1

  2

  a
• B．

  2

  2

  a
• C．

  3

  2

  a
• D．a

Answer 1

分析：取AC的中点E，连接DE，BE，根据正方形可知EB⊥AC，ED⊥AC，则∠BED为二面角B-AC-D的平面角，在三角形BDE中求出BD的长．

解答：解：AD=DC=AB=BC=a，

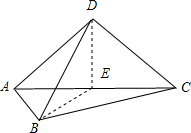
取AC的中点E，连接DE，BE，DE=BE=

2

2

a．
∵ABCD是正方形，
∴EB⊥AC，ED⊥AC，
∴∠BED为二面角B-AC-D的平面角，
∴∠BED=90°
∴BD=

DE2+BE2

=a．
故选：D

点评：本题的考点是与二面角有关的立体几何综合问题，主要考查在折叠问题中考查两点间的距离．关键是折叠问题要注意分清在折叠前后哪些量发生了变化，哪些量没变．